Táquions
ARTIGO /
Erasmo Recami* //
Há mais de 40 anos, o físico italiano Erasmo Recami e seus colaboradores vêm desenvolvendo uma teoria para explicar fenômenos superluminais compatíveis com as demais teorias já bem estabelecidas. De acordo com seus trabalhos, uma teoria sem paradoxos para táquions pode ser formulada e testada. Recentemente, a possível existência de fenômenos superluminais ganhou força pelos resultados de importantes experimentos que corroboram sua teoria.
– – – – –
Se os táquions existem, seria preciso encontrá-los;
se não existem, seria necessário explicar porquê.
E. Sudarshan
Apresentação
Desde tempos remotos, a imaginação dos físicos é atraída pela possível existência de partículas que viajam no vácuo com velocidades superiores a da luz. De acordo com nosso conhecimento, Lucrécio (aproximadamente 50 a.C.) foi o primeiro a se referir, em De Rerum Natura, a objetos que iam mais rápido e mais longe, e percorriam mais espaço no mesmo tempo, que os raios de sol quando estes atravessavam os céus. Ao longo dos séculos houve muita especulação sobre esta ideia, sugerida – entre outros – por J. J. Thomson (1889), O. Heaviside (1892) e, especialmente, pelo grande A. Sommerfeld (1904 e 1905). Enquanto isso, por razões que serão discutidas a seguir, o advento da teoria da relatividade especial, formulada por Albert Einstein, em 1905, difundiu a crença de que a velocidade da luz no vácuo é o limite superior de todas as velocidades no universo. Em 1917, R. C. Tolman considerou ter demonstrado que a existência de partículas mais rápidas que a luz levaria a um paradoxo: a possibilidade de transmitir informações para o passado ou o “anti-telefone”.
Tais convicções inibiram durante várias décadas as iniciativas de pesquisa sobre velocidades superluminais. Além de um trabalho isolado do matemático italiano Somigliana, os primeiros estudos, no século passado, que reformularam a questão foram contribuições do francês H. Arzeliès (1955 e 1958), do alemão H. Schmidt (1958), do japonês S. Tanaka (1960), do soviético Y. P. Terletsky (1960) e, principalmente, do indiano E. C. George Sudarshan e seus colaboradores (1962). O caminho aberto por este último foi seguido por muitos pesquisadores, entre os quais se destacam Jones e Feinberg, nos Estados Unidos, e o autor deste artigo e seus colaboradores, na Europa. Entre 1963 e 1966, no Instituto Nobel, Alväger conduziu as primeiras investigações experimentais destinadas a detectar partículas superluminais, batizadas por Feinberg de táquions (do grego taxús – ταχùς – breve, rápido). Chamamos de lúxons (do latim lux) as partículas que viajam com velocidades exatamente iguais a da luz, como os fótons, e por último usamos o termo brádions (do grego bradús – βραδùς – lento) para designar objetos subluminais.
Recentemente, vários resultados experimentais parecem sugerir a possível existência de objetos que viajam a uma velocidade maior do que c, a velocidade da luz no vácuo. Enumeraremos alguns no final do artigo, mas mencionaremos apenas um neste momento. Considere uma onda eletromagnética, por exemplo, uma de rádio que viaje ao longo de uma guia metálica de ondas, como uma antena de um receptor; as leis da física estabelecem que, se a seção transversal da guia é feita muito estreita, a onda não pode avançar. A teoria matemática que se refere a esta situação postula que a onda continuará, mas com energia ou impulso imaginários, ou seja, em forma de onda evanescentes. Há muito tempo, suspeitava-se que as ondas evanescentes possuíssem velocidade de grupo que excede a c, fato que foi verificado em Colônia por Nimtz e seus colaboradores (1992), e confirmado pouco tempo depois, utilizando-se diferentes condições experimentais, por Chiao, Kwiat, Steinberg, da Universidade da Califórnia, em Berkeley, que divulgaram o resultado na Scientific American de agosto de 1993. No mesmo ano, Ranfagni e colaboradores também encontraram, num experimento realizado em Florença, que as ondas evanescentes viajam a velocidades superiores a c.
Relatividade especial, causalidade e táquions
A relatividade especial – que tem sido exaustivamente verificada e constitui, juntamente com a mecânica quântica, um dos pilares da física moderna – fundamenta-se em termos de dois postulados: (a) as leis da mecânica e do eletromagnetismo devem ser as mesmas (isto é, são invariantes na forma) para todos os observadores inerciais (ou seja, aquelas cujo movimento é retilíneo e uniforme em relação ao chamado céu de estrelas fixas, e, portanto, uns em relação aos outros), e (b) o tempo e o espaço são homogêneos, e o espaço ou o vazio é isotrópico (tem as mesmas propriedades em todas as direções). Einstein demonstrou que, quando as distâncias e as velocidades relativas são muito grandes, dois eventos (ou acontecimentos) da vida de um objeto pode aparecer, para observadores distintos, separados por uma distância espacial (Δx) e temporal (Δt) também diferentes. Os dois postulados enunciados permitem chegar a um conclusão importante: deve haver uma – e apenas uma – velocidade invariável (c), tal que seu quadrado tem o mesmo valor para todos os observadores inerciais. Como se sabe, verificou-se experimentalmente que esta tem um valor finito e equivale à velocidade da luz no vácuo, de modo que: c + v = c. De passagem, note que a velocidade infinita, se houver, não seria invariante: ∞ + v = V, onde V ≠ ∞; a operação ‘+’ não corresponde, no caso de composição de velocidades, a operação de soma aritmética.
Uma das consequências da relatividade especial é que, com o aumento da velocidade (v), a energia total (E) de uma partícula subluminal de massa de repouso m0 aumenta de acordo com:
 (1)
(1)
Quando v tende a c, o denominador da fração tende a zero, fazendo a energia E tender a infinito. Portanto, forças infinitas seriam necessárias para fazer com que um brádion atingisse a velocidade da luz, o que levou à opinião, bastante difundida, de que tal velocidade não pode ser alcançada, muito menos superada.
No entanto, contrariamente ao que as aparências sugerem, isso não esgota a questão. Assim como existem partículas que viajam à velocidade da luz, sem que a tenham alcançado acelerando-se a partir de velocidades subluminais, também poderiam existir outras que sempre viajaram com velocidades superiores a c. Isto foi ilustrado por Sudarshan pitorescamente: suponhamos que um demógrafo que estuda a população da Índia afirme, ingenuamente, que ninguém vive ao norte do Himalaia, uma vez que nunca conseguiu-se atravessar essas montanhas. Assim nos depararíamos com uma conclusão absurda. As populações da Ásia Central nasceram e vivem além dos Himalaias: não precisam nascer na Índia e, então, atravessar as montanhas. O mesmo pode acontecer com partículas mais veloz que a luz.
O desafio agora é mostrar que o problema pode ser colocado, de modo pertinente, no âmbito da física contemporânea. Para isso, faremos uma breve revisão dos princípios da relatividade especial, considerando partículas subluminais e superluminais, começando pelas primeiras. Contrariamente à física clássica, a teoria da relatividade postula que medições do espaço e do tempo não são independentes entre elas. Não é possível descrever o universo em termos puramente espaciais, uma vez que a simultaneidade é relativa ao observador: o que para um acontece em um certo instante, para outro é uma série de eventos que ocorrem em momentos diferentes.
As distâncias espaciais e temporais entre dois eventos na vida de um objeto variam de acordo com o ponto de vista de diferentes observadores. Nem o espaço nem o tempo podem ser considerados separadamente parâmetros físicos estritamente objetivos, de modo que torna-se necessário construir um novo conceito de distância. Partindo de quantidades relativas a cada observador, a relatividade especial ensina a definir quantidades absolutas, tal que quaisquer dois eventos aparecem separados por uma distância espaço-temporal Δs de mesmo valor para todos os observadores, o que faz com que, de alguma forma, o nome da teoria torne-se inapropriado, já que seria melhor denominá-la teoria da absolutividade.
A distância espaço-temporal Δs é definida pela relação Δs2 = c2. Δt2-Δx2, que generaliza o teorema de Pitágoras para quatro dimensões. É fácil ver que: Δs2> 0 para brádion (chamado caso tipo-tempo); Δs2 = 0 para um lúxon (caso tipo-luz), e Δs2 <0 para um táquion (caso tipo-espaço). Para os brádions, que percorrem pouco espaço em muito tempo, predomina o sinal positivo de c2. Δt2. Os táquions percorrem muito espaço em pouco tempo: para eles predomina o sinal negativo de Δx2. No caso tipo-luz, o intervalo é zero. No que se segue, quando conveniente, usaremos c como unidade de medida de velocidades.
A relatividade especial não pode ser concebida mediante sistemas definidos apenas por suas coordenadas espaciais e temporais. É preciso, também, considerar um espaço dual, definido por coordenadas de energia (E) e momentum (p). Passando de espaço-tempo para energia-momentum, podemos antecipar que a quantidade E2 – p2 (análoga a Δs2 do primeiro espaço) terá o mesmo valor em todos os sistemas inerciais, ou seja:
no caso de um brádion E2 – p2 = + m02 > 0 (2a)
no caso de um lúxon E2 – p2 = 0 (2b)
no caso de um táquion E2 – p2 = – m02 < 0 (2c)
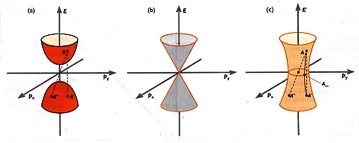
A Figura 1 mostra, no espaço de energia-momento (E, p), como as relações acima representam, respectivamente: para brádions, um hiperbolóide de duas folhas, simétrico em relação ao eixo E; para lúxons, um duplo cone, e para táquions, um hiperbolóide de rotação de uma folha. Salta aos olhos que os brádions e os táquions livres estão sujeitos a relações diferentes: os primeiros podem ter momentum nulo, no caso em que possuem a energia mínima (E0 = m0.c2), a qual nunca é igual a zero; os segundos, por sua vez, podem ter energia total zero, e então aparecem com impulso mínimo (|p|≡ p0 = m0c) que, por sua vez, nunca é zero. Além disso, lembrando que v = p/E, também pode-se verificar que os táquions dotados de velocidade infinita – chamados táquions transcendentes – transportam energia nula. Logo, nenhuma destas partículas poderiam transmitir energia com velocidade infinita.
Fig. 1: Modelo a três dimensões das superfícies E2 – p2 = ± m02: para brádions (a); para lúxons (b); para táquions (c); por razões óbvias, as figuras foram construídas considerando pz= 0. Dado que uma transformação ordinária de Lorentz determina a passagem de um ponto a outro da mesma folha de hiperbolóides, o caráter de matéria ou antimatéria é absoluto no caso dos brádions, mas relativo ao observador no caso dos táquions.
Finalmente, da equação (2c) podemos deduzir que, para os táquions, a fórmula (1) passa a ser:
 (3)
(3)
Assim, a equação descreve o comportamento descrito na Figura 2, no caso em que |v| é maior que c. Consequentemente, táquions – se houver – possuem a notável propriedade de aumentar a sua velocidade quando sua energia total diminui e vice-versa. Portanto, como vimos, quando sua velocidade se aproxima de infinito, a energia total tende a zero. Por outro lado, para reduzir a velocidade de um táquion até o limite inferior c são necessárias forças gigantescas. Desta forma, c continua sendo um limite de velocidade que não pode ser atravessado vindo por cima (à direita da Figura 2) ou abaixo (à esquerda da Figura 2). Se para os brádions a velocidade da luz representa um limite superior das velocidades que podem chegar, para os táquions é o limite inferior. É bom lembrar que estamos analisando partículas subluminais e superluminais, mas temos apenas considerado observadores comuns, movendo-se a velocidades subluminais. Mais tarde, estenderemos o sistema de referência.

Fig. 2: O gráfico relaciona – para brádions (v < c) e táquions (v > c) – a energia total relativista com a velocidade. Para simplificar, tomamos uma velocidade na direção do eixo x do sistema de referência. Claramente, em ambos os casos, a quantidade de energia tende a infinito quando as partículas se aproximam da velocidade da luz, seja pela esquerda ou pela direita.
Nos referimos de passagem, para conciliar a existência de táquions com o princípio da causalidade, a expressão que na literatura científica consiste de duas declarações independentes: não podem existir sinais superluminais, – postulado que, obviamente, abandonamos – e que a causa antecedente, no tempo, o efeito, é o que define uma causalidade retardada – que adotaremos.
Pensava-se que táquions violavam a causalidade, pois, em um sistema, eles eram emitidos por A e absorvidos por B, enquanto que para outros observadores eram antipartículas emitidas por B e absorvidas por A. Mas o princípio de reinterpretação elimina o paradoxo de transporte de informação para trás no tempo, mas o faz sacrificando a antiga convicção de que relações de causa e efeito são independentes do observador. No exemplo acima, um observador julgará que o evento ocorrido em A era causa do que aconteceu então em B, enquanto que o outro pensará o contrário. Ambos verão, no entanto, que o que consideram causa antecede no tempo o que consideram efeito.
Mais uma vez, a reflexão sobre os táquions requer uma crítica de nossos preconceitos. Se aceitarmos que para todos os observadores os fenômenos devem respeitar a lei de causalidade, então não podemos exigir que certos detalhes descritivos (neste caso os rótulos de causa e efeito) sejam também inalterados.
Sabemos que não é fácil aceitar a ideia de que ser causa ou efeito depende do observador. Talvez possa reduzir o incômodo que provoca analisando uma situação que ocasiona dificuldades semelhantes, mas que está alheia aos preconceitos atuais. Os antigos egípcios não conheciam outros rios além do Nilo e seus afluentes. Como todos fluíam do sul para o norte, os conceitos de sul e contra a corrente, bem como o norte e a favor da corrente, eram equivalentes. Quando descobriram o Eufrates – que corre do norte para o sul – houve uma enorme crise conceitual; o obelisco de Tutmés I faz referência à corrente invertida, que vai contra a corrente, mesmo quando move-se a jusante. Quando nos deparamos com os táquions, nossa situação é semelhante a dos antigos egípcios. Uma vez admitido que esses existem, relativiza-se o modo de conceber o que é causa e o que é efeito, e uma série de paradoxos que, apesar de terem solução (pelo menos na microfísica), alimentam muitas dúvidas.
Até agora consideramos partículas com qualquer velocidade, mas temos sempre nos referido a observadores subluminais. Tentaremos agora estender a nossa análise a todos os sistemas inerciais, incluindo, se possível, aqueles que, em relação aos sistemas ordinários viajando com velocidades superluminais. Na verdade, as expressões subluminal e superluminal têm, elas mesmas, um significado relativo, pois nós mesmos, para um observador taquiônico S, formamos um sistema superluminal. Para estender a relatividade especial a nosso objeto de estudo, é preciso postular que todos os observadores inerciais (subluminais ou superluminais) são equivalentes. Em particular, assumimos que, como nós, observadores taquiônicos também têm à sua disposição instrumentos de medição, partículas e todos os demais elementos próprios da nossa física. Obviamente, os brádions, assim como os objetos em repouso relativos ao nosso sistema de referência, são táquions para os sistemas S e vice-versa. Portanto, a velocidade da luz (c) continuará inalterada em todos os sistemas inerciais, mesmo os superluminais.
Algumas evidências experimentais
Em primeiro lugar, vale destacar uma série de experimentos iniciados em 1971 e que envolvem o estudo de neutrinos, partículas sem carga elétrica e com massa que se supõe extremamente pequena. Esses experimentos parecem indicar que o quadrado da massa de uma das três variedades de neutrinos (mais especificamente, neutrinos associados à partícula múon) é negativo. Mais recentemente, outros resultados parecem indicar que também seja negativo o quadrado da massa de uma segunda variedade de neutrinos, aqueles associados ao elétron. Em ambos os casos, essa relação equivaleria a dizer que esses neutrinos são taquiônicos ou, pelo menos, que em boa parte sejam taquiônicos. Dentre esses experimentos está o resultado referente ao experimento OPERA (2011) de grande repercussão.
Em segundo lugar, outras observações, também experimentais, feitas desde 1971, mas dessa vez em astrofísica, têm revelado a presença de objetos muito velozes expelidos pelo núcleo de vários quasares. Caso os quasares estejam muito distantes da Terra como geralmente é aceito, essas velocidades de expulsão seriam então superluminais. Porém, alguns autores renomados, como o astrofísico norte-americano Harlton Arp, alertaram para o fato de que os quasares podem estar mais próximos de nós que o previsto. E, nesse caso, as velocidades em questão poderiam ser subluminais. Nos últimos anos, no entanto, têm sido descobertas expansões superluminais aparentes no interior de certos objetos celestes provisoriamente batizados microquasares que habitam a Via Láctea, a nossa galáxia. E, nesse caso, as incertezas sobre as distâncias são de pouca importância. Assim, as expansões observadas poderiam ser superluminais mesmo que tenham sido tentadas interpretações mais ortodoxas.
Em terceiro lugar, no âmbito da mecânica quântica (teoria que rege os fenômenos na dimensão das moléculas e dos átomos e suas subpartículas), experimentos têm verificado que um fenômeno peculiar do mundo quântico ocorre com velocidade superior a c. Denominado efeito de tunelamento, esse fenômeno tem a ver com a propriedade de partículas subatômicas e de fótons conseguirem atravessar certas barreiras – forças de repulsão elétrica ou forças nucleares de coesão, por exemplo –, sem ter energia suficiente para isso. Experimentos feitos a partir de 1992 verificaram que esses processos ocorrem mesmo com velocidades taquiônicas. Essas experiências foram feitas, no caso dos fótons, pelo físico alemão Guenter Nintz, na Universidade de Colônia (Alemanha), pelo grupo de Ray Chiao e Aephraim Steinberg, da Universidade de Berkeley (Estados Unidos), por Anedio Ranfagni e colaboradores, na Universidade de Florença (Itália), e por outros pesquisadores em Viena (Áustria), além de Orsay e Rennes (França). Esses resultados ganharam vasta repercussão na comunidade científica internacional, bem como na mídia e na literatura não especializada. Foram noticiados pelas revistas de divulgação científica Scientific American (Estados Unidos) e New Scientist (Grã-Bretanha), bem como pela revista semanal Newsweek. Vale notar que, do ponto de vista da física clássica, fótons em tunelamento são, na verdade, um tipo particular de ondas eletromagnéticas (denominadas ondas evanescentes). E que também, a partir da relatividade estendida, já se sabia que essas ondas tinham velocidade maior que c, como foi confirmado através de simulações numéricas. Tudo parece então autoconsistente!
Finalmente, em quarto lugar, deixando de lado outros ramos do conhecimento, alguns grupos de engenheiros, entre eles, os chefiados respectivamente por Jian-yu Lu, Amr Shaarawi e Peeter Saari descobriram, em uma série de belos trabalhos, que as equações que descrevem o comportamento das ondas, tanto mecânicas (som, por exemplo) quanto eletromagnéticas (luz), admitem novas soluções, tanto subluminais quanto superluminais, além daquelas já conhecidas. Esses pesquisadores têm explicado em detalhes como gerar essas novas configurações de ondas, por exemplo, as superluminais e as produziram em experimentos com ondas acústicas e ópticas. Essas ondas se propagam, no meio considerado, com velocidades maiores que a do som, no primeiro caso, e que a da luz, no segundo. Além disso, elas se deslocam quase sem distorção, mais uma propriedade muito útil em vários desdobramentos práticos dessa descoberta.
Ondas em forma de ‘X’
Outros experimentos interessantes estão em andamento, por exemplo, nos laboratórios de pesquisa da Pirelli Cabos, em Milão (Itália), usando como fonte pulsos de laser, bem como na Faculdade de Engenharia Elétrica da Universidade Estadual de Campinas. Mais uma confirmação experimental, feita a partir de uma sugestão do autor deste artigo, realizou-se em um laboratório do Conselho Nacional de Pesquisas da Itália, em Florença, dessa vez usando microondas (assim como a luz, as microondas também são ondas eletromagnéticas). O experimento foi feito pelos pesquisadores italianos Daniela Mugnai, Anesio Ranfagni e Rocco Ruggeri, tendo sido publicado na revista especializada Physical Review Letters de 22 de maio de 2000. Esse experimento obteve vasta repercussão na imprensa internacional, juntamente com o trabalho de Lijung Wang e colaboradores, feito no instituto de pesquisas NEC, em Princeton (Estados Unidos), e publicado na revista científica Nature de 20 de julho de 2000. Essas ondas superluminais (ou supersônicas), tendo tipicamente a forma de X, preditas em 1980 com base na relatividade estendida, são até o momento a melhor verificação dessa teoria. É curioso saber que a primeira aplicação dessas ondas de tipo X, justamente por causa de sua propriedade de movimento quase sem deformação, está em progresso na área médica, precisamente no campo da imagem por ultra-sonografia. Há apenas alguns anos, a hipótese de que os táquions poderiam ser usados para a obtenção direta de ecografias em três dimensões teria levantado a incredulidade de qualquer físico, incluindo o que assina este artigo.
Considerações finais
Vale lembrar que, embora sempre viajando com velocidade superluminal, os táquions não emitem radiação Cherenkov no vácuo. Muitas investigações experimentais têm se baseado na hipótese contrária, o que é errado.
A possível existência de objetos superluminais também interessa à cosmologia. Sabemos, por exemplo, que quando uma fonte de ondas eletromagnéticas (ƒ0) tende a afastar-se com a velocidade luz, a frequência da radiação observada ƒ tende a zero. Portanto, o fato da radiação originada em fonte superluminal que se afasta de nós, se existir, ser novamente percebida e o aparecimento de frequências negativas quando a fonte se aproxima com velocidade superluminal são ilustrados nas Figuras 3 e 4.

Fig. 3: Extensão da lei de Doppler. Gráfico da frequência em função da velocidade.

Fig. 4: Emissão proveniente de fonte superluminais.
Para concluir estas considerações sobre a teoria dos táquions, consideramos oportuno comentar alguns aspectos notáveis de interesse:
(a) a extensão do eletromagnetismo aos táquions fornece uma conexão interessante entre essas partículas e os monopolos magnéticos;
(b) no âmbito da relatividade geral, os táquions – se existirem – poderiam fornecer informações do interior dos buracos negros, os quais não permitem que partículas que se movem com velocidade menores ou iguais a da luz escapem;
(c) os táquions podem desempenhar um papel fundamental como intermediários das interações entre partículas elementares, e também ocupar um lugar de destaque na mecânica quântica;
(d) em vários quasares, assim como em algumas galáxias, há quase 30 anos observa-se expansões que ocorrem a velocidades aparentemente cinquenta vezes maior do que a da luz. A partir de nós, as distâncias a estas galáxias e quasares não é bem compreendida, mas se fossem muito inferiores às supostas, tais expansões anômalas poderiam corresponder a velocidades ordinárias. Em setembro de 1994, a revista Nature publicou um artigo sobre uma expansão superluminal observada em um objeto cuja distância é bem conhecida, pertencente à nossa própria galáxia;
(e) também há 30 anos foi verificado experimentalmente que os neutrinos do múon parecem obedecer a relação (2c), descrita anteriormente. Recentemente, o mesmo fenômeno foi constatado experimentalmente para neutrinos do elétron. Estes fatos indicam que os neutrinos têm um pouco mais do que a velocidade da luz no vácuo.
A física teórica do século XX levou naturalmente à formulação de hipóteses sobre a existência de vários tipos de partículas que nunca foram observadas (monopolos magnéticos, quarks, táquions). Muitos setores da física não podem avançar sem eles, por isso é necessário retornar às ideias dos gregos da era clássica: de acordo com Demócrito de Abdera, qualquer coisa que pudesse ser pensada de forma não-contraditória deveria existir em algum lugar de um universo ilimitado. Este conceito, recentemente adotado por Gellmann Murray com o nome de princípio totalitário, adquiriu uma formulação jocosa: tudo o que não é proibido, é obrigatório. O que nos traz de volta as palavras de E. C. George Sudarshan colocado como epígrafe neste texto: “se os táquions existem, seria preciso encontrá-los; se não existem, seria necessário explicar porquê”.
– – – – –
*Erasmo Recami é doutor pela Università Statale di Milano (1964) e pelo Istituto Nazionale di Fisica Nucleare (1967). Foi Professor Titular pela Universidade Estadual de Campinas (Unicamp) no período de 1984 a 1994. Atualmente é professor do INFN-Sezione di Milano (Milão), da Università degli Studi di Bergamo, Itália e professor visitante estrangeiro (PVE) da CAPES c/o o DMO/FEEC da Unicamp, Brasil. Possui mais de 70 trabalhos publicados e diversas colaborações, em particular, com físicos brasileiros teóricos e experimentais.
O autor gentilmente agradece a Eduardo Bittencourt pela edição do presente texto, a Mário Novello e aos demais representantes do comitê editorial da revista Cosmos e Contexto pelo convite, e aos colaboradores M. Z. Rached, M. E. Vasconselos, M. F. Decker, H. E. Hernandez-Figueroa e C. Castro.
– – – – –
Leituras sugeridas
RECAMI, E.; RACHED, M. Z. Mais velozes que a luz? Ciência Hoje, v. 29, n. 170, p. 20, 2001.
GIANNETTO, E.; MACCARRONE, G. D.; MIGNANI, R.; RECAMI, E. Are Muon Neutrinos faster-than-light Particles? Physics Letters B, 178, p. 115, 1986.
RECAMI, E. Extended special relativity: a review (Classical tachyons and possible applications). Rivista Nuovo Cimento, v. 9, n. 6, 1986.
RECAMI, E. I Tachioni. Annuario 73, Enciclopédia EST-Mondadori. (Ed. E. Macorini). Mondadori: Milão, p. 85, 1973.
RECAMI, E. Superluminal tunneling through successive barriers. Does QM predict infinite group-velocities? Journal of modern optics, 51, p. 913, 2004.
FIGUEROA, H. E. H.; RACHED, M. Z.; RECAMI, E. (editores). Localized Waves. J. Wiley: Nova York, 2008.