Lições de Cosmologia para não-especialistas (das leis físicas às leis cósmicas) – 4

Estas notas constituem uma extensão de um curso de cinco lições que dei em 2018 no Centro Brasileiro de Pesquisas Físicas para divulgar alguns aspectos do universo que os cientistas têm elaborado nas últimas décadas, sem me deter nas demonstrações matemáticas associadas. Aqueles que tiverem interesse em aprofundar este conhecimento técnico poderão consultar as referências citadas.

Jamais, jamais concluir uma paz com o dogma

(Hegel)

TERCEIRA LIÇÃO.  A QUESTÃO CAUSAL

Ao instaurar uma nova relação causal no mundo a partir da existência de uma velocidade máxima intransponível no mundo, os físicos do início do século XX consideraram a proposta da relatividade especial como padrão e a extensão desse princípio causal ao universo como natural.

Eles não tiraram todas as consequências do procedimento descoberto por Gauss na construção de um tempo global. Foi preciso a entrada em cena de um outro matemático, Kurt Gödel, para que pudéssemos entender de modo direto a relação segundo a qual, causalidade local não implica causalidade global.

Dito de outro modo, é possível em cada ponto da trajetória de um corpo obedecer a regra da relatividade especial caminhando somente no interior do cone de luz local e no entanto violar a regra causal globalmente.

Isso é possível, pois na presença de um campo gravitacional, descrito pela teoria da Relatividade Geral, ocorrem alterações no cone de luz devido a propriedades da geometria.

Ou seja, a luz, como tudo que existe, sofre efeito gravitacional. Assim, a alteração provocada pela interação gravitacional sobre o cone de luz é capaz de impedir a extensão da causalidade local para todo o espaço-tempo. Nem toda geometria possui essa propriedade. Por exemplo, nas geometrias que representam o campo gravitacional de uma estrela ou na cosmologia de Friedmann, essa dificuldade não aparece. No entanto, essa independência da causalidade local com a causalidade global aparece claramente em alguns tipos de campos gravitacionais.

O primeiro exemplo, e o mais contundente foi apresentado por Gödel. Vamos nos dedicar um pouco a examinar essa geometria pois embora ela possa não estar relacionada ao universo atual, ela mostra certas características que são importantes de ter em mente se quisermos ir além de um conhecimento superficial do universo.

A geometria de Gödel tem como fonte a mesma estrutura que a de Einstein, ou seja, matéria constante representada por um fluido perfeito de densidade de energia E além de uma misteriosa constante cosmológica Λ. Em ambos os casos a geometria é estática, independente do tempo. A principal diferença entre elas está nas características cinemáticas da fonte. No caso do modelo cosmológico de Einstein o fluido está em repouso total; no caso de Gödel, o fluido possui uma rotação local (não se trata de uma rotação da matéria global, pois não existe “o lado de fora”)ou seja em cada ponto ele gira com velocidade de rotação constante.

É precisamente essa vorticidade que dá ao modelo cosmológico de Gödel suas estranhas propriedades. Para tentarmos visualizar um pouco essa estrutura da métrica de Gödel, vamos descrevê-la em um sistema de coordenadas cilíndrico. O leitor interessado em detalhes deve consultar o livro A máquina do tempo (um olhar científico sobre viagens não convencionais no tempo) ou, para mais detalhes técnicos, no artigo (ver referências) de Novello, Soares e Tiomno.

Causalidade local (Teoria da Relatividade Especial)

A Teoria da Relatividade Especial alterou a ideia newtoniana de um tempo único absoluto e em seu lugar, concedeu a cada observador (a cada corpo) um “seu” tempo próprio. Isso foi consequência da existência de uma velocidade máxima absoluta (da luz).  Considerando a velocidade da luz:

o caminho da luz (neste gráfico) é dado pela reta de inclinação 45°.

Um gráfico bem simples mostra que todo e qualquer corpo se movimenta com velocidade inferior à da luz. Considerando não somente o plano (t,x) podemos representar os caminhos da luz por um cone. A luz se propaga sobre a superfície do cone.

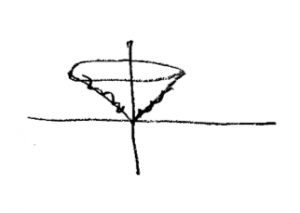
A transformação entre relógios para observadores inerciais é o território onde se estabelece a Relatividade Especial. Há uma regra que permite comparar esses tempos não idênticos.

Note que como optou-se por descrever os eventos em um cenário quadri-dimensional (três dimensões de espaço e uma de tempo), passar de uma representação à outra é substituir os valores da caracterização de um fenômeno em  por outro conjunto estabelecida por Lorentz, Poincaré e Einstein sintetizados  por este último na teoria da Relatividade Especial.

A principal novidade dessa descrição espaço-temporal está relacionada ao fato de que a distância entre dois eventos não obedece mais à regra euclidiana tridimensional de ser sempre positiva. Isso se deve a que o tempo aparece nas formulas de distância espaço-temporal atribuindo-se, por convenção,  um valor negativo à sua medida. A formula que determina a soma dos quadrados de uma distância espacial na geometria de Euclides se escreve

Ela é substituída no espaço-tempo quadridimensional por uma outra na qual o tempo entra com sinal oposto a essas quantidades espaciais, uma possibilidade examinada pelo matemático alemão Bernhard  Riemann que generalizou a expressão da distância entre dois pontos em uma variedade tendo um número arbitrário e finito de dimensão. No caso da Relatividade Especial ( entendida como o limite local, pontual, de qualquer geometria descrita na Relatividade Geral) um desses termos é negativo e os demais positivos ou vice-versa, isto é, três são negativos e um é positivo. Vamos escolher essa última forma e escrever

Note que deveria aparecer uma constante à frente do termo temporal para que toda a formula tivesse dimensionalidade correta de comprimento ao quadrado. Estaremos subentendendo que a velocidade da luz c que deveria multiplicar o termo temporal é, por convenção, definida como tendo o valor unitário.

Assim, reconhecemos 3 tipos de distâncias, conforme a figura:

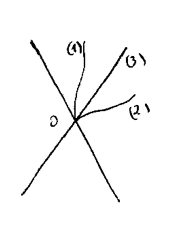
01: Distância tipo-tempo;

02: Distância tipo-espaço;

03: Distância tipo-luz (ou tipo nula).

Assim os valores respectivos das distâncias são, respectivamente,

d(01) é positiva;

d(02) é negativa;

d(03) é nula.

Isso decorre da convenção que fizemos da representação.

Como somente corpos percorrendo caminhos com velocidade menor que a da luz é permissível, vemos que estes caminhos são tipo-tempo (d(01)).

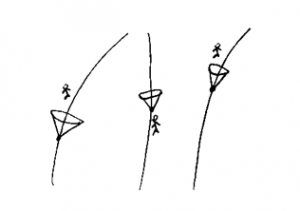
Miríades de observadores com seus correspondentes tempos e suas correspondentes relações causais.

A causalidade é definida então, com a afirmação de que corpos reais só podem viajar no interior do cone de luz de cada ponto.

É possível coordenar esses tempos e descrever o Espaço-tempo (ET) com um só tempo? Gauss (matemático alemão) mostrou que isso é sempre possível, pelo menos em uma região compacta do ET. E em todo o ET?

Causalidade global (Teoria da Relatividade Geral)

Em sua primeira descrição da cosmologia, Einstein em 1917, considerou a hipótese de que nosso universo admite uma tal separação espaço + tempo. Tratava-se então de conservar o máximo possível da versão simples contida no cenário newtoniano.

A cosmologia atual manteve, nesses 100 anos, essa hipótese. Somente uma exceção notável ocorreu, graças ao matemático Kurt Gödel e uns poucos seguidores.

Comecemos por considerar a hipótese cosmológica da possibilidade de fixarmos um tempo cósmico global, onde teríamos a seguinte configuração:

Para que essa hipótese seja verdadeiramente possível é necessário examinar o que acontece em todo o espaço-tempo.  Gödel argumentou de outra forma e mostrou explicitamente que a causalidade local não implica causalidade global.

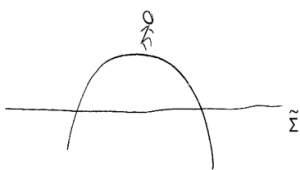
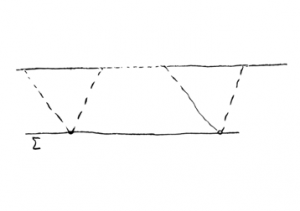
Note na figura anexa um exemplo simples de contradição com a hipótese do tempo único, onde um observador, contrariamente ao que a figura anterior sugere, pode cruzar duas vezes uma dada superfície como a .

Um observador que cruza duas vezes  cria um conflito causal que Gödel descreve de modo claro e simples.  A argumentação de Gödel é a seguinte. Observemos que, como toda forma de energia, a luz também é influenciada por um campo gravitacional. Ou seja, a luz pesa, isto é, a gravitação altera a sua propagação. Pode-se então imaginar uma situação onde essa propagação permite a estranha configuração (ver gráfico) de um observador passar mais de uma vez através dessa superfície .

Se a curva do tipo-tempo, é fechada, então:

• Localmente, o observador que caminha sobre ela afirma a validade causal, isto é, ele sempre caminha para seu futuro local;
• Globalmente, ela se fecha sobre si mesma, ou seja, passa duas vezes pelo mesmo ponto no espaço-tempo. Trata-se de uma violação da relação causal globalmente. Gödel mostrou que esses caminhos existem em algumas geometrias permitidas pela Relatividade Geral, isto é, que satisfazem as equações dessa teoria. Mais tarde outras geometrias, tendo propriedade análogas, foram encontradas, algumas delas não sendo estáticas como a descoberta por Gödel, tendo dependência temporal.

Comentário adicional: em todas as geometrias conhecidas que possuem essa propriedade gödeliana, os observadores fundamentais (isto é, aqueles que se movimentam ao longo dos caminhos determinados pela fonte dessas geometrias) possuem rotação (vorticidade). Parece assim que a rotação é uma característica facilitadora da presença de curvas tipo-tempo fechadas (CTC, sua sigla em inglês).

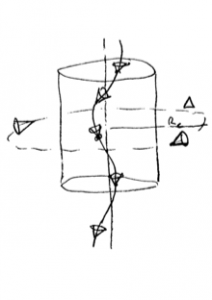
Como exemplo concreto das ideias de Gauss é possível exibir uma propriedade notável dessa geometria de Gödel (bem como de outras, exibindo CTC). Vamos representar a geometria de Gödel em um sistema de coordenadas cilíndrico, como na figura. É possível mostrar que existe um raio crítico a partir de um ponto dessa geometria (em verdade, de qualquer ponto, pois ela é homogênea), tal que em seu interior a representação gaussiana de tempo único seja válida. Somente para além de , é possível existir uma curva fechada do tipo tempo. Encontramos aqui um exemplo concreto da afirmação de Gauss, segundo o qual em qualquer geometria é sempre possível construir um sistema de coordenadas global (gaussiano) com um tempo único válido no domínio compacto .

A questão do horizonte no universo de Friedmann

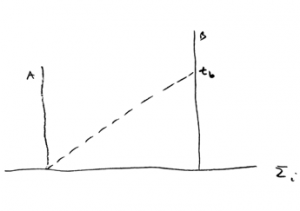
A existência de um limite máximo para a velocidade de propagação de informação (a luz) implica que cada corpo, cada observador, tem em cada instante a possibilidade de acesso somente a uma parte limitada do universo. Assim, o observador B na figura abaixo só recebe informação do que aconteceu com o corpo A no tempo no instante . Ou seja, cada corpo possui um seu horizonte delimitado pelo seu cône de luz.

Considere agora um cenário onde em um caso particular de modelo cosmológico do tipo de Friedmann o universo possui um começo (big bang) e um fim em um tempo de duração finita.

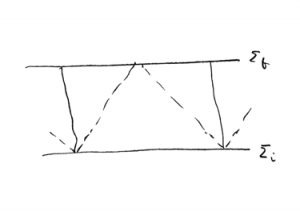
Veja na figura anexa, a representação de dois corpos A e B em um modelo de universo possuindo começo em e fim em .  Dependendo da distância espacial entre A e B no instante inicial eles podem nunca trocarem informações. Isto é, durante o tempo de duração desse hipotético universo finito, eles não saberão da existência um do outro.

Teoria das representações:  sistema de coordenadas

Na teoria das representações aprendemos como identificar boas descrições que exibem as características de um dado fenômeno independentemente do observador permitindo a separação de suas propriedades com a linguagem usada para fazer comentários sobre ele.

Sabíamos de longa data que ao descrevermos um fenômeno no espaço e no tempo, é condição preliminar que fixemos (arbitrariamente) um dado sistema de coordenadas com o qual iremos identificar onde e quando um dado processo ocorre. A descrição do fenômeno guarda assim informação do processo no mundo bem como a escolha particular de coordenadas empregadas.

Desde os primeiros passos na mecânica clássica dos corpos essa escolha exerceu um importante papel, pois a simetria de um dado fenômeno induz naturalmente escolhas mais convenientes. Assim, por exemplo, posso usar coordenadas cartesianas para fixar pontos, lugares, na superfície de uma bola. No entanto, é mais conveniente escolher coordenadas esféricas, pois desse modo essa caracterização torna essa tarefa mais simples. Ou seja, existem sistemas de coordenadas mais adaptados do que outros para cada fenômeno.

Esse procedimento foi generalizado para o espaço-tempo da relatividade especial de Poincaré-Einstein e mais tarde para a relatividade geral de Einstein.

Em síntese, uma descrição de um fenômeno só pode ser admitida como verdadeira se contiver características comuns a todos os sistemas de representação. Ou, dito de outro modo, as características que sejam invariantes sob transformações arbitrárias de coordenadas.

Sabendo dessa dificuldade de princípio, os físicos fizeram da análise da representação um importante tópico de sua disciplina. Essa análise obteve um sucesso notável no século XX com o surgimento da teoria da relatividade (especial e geral) que colocou em evidência um procedimento simples para retirar da descrição dos fenômenos a dependência particular com o modo de escolha de coordenadas. 

Escolha de representação

Além do sistema de coordenadas para obter as boas variáveis devemos caracterizar a própria estrutura onde os fenômenos são descritos, ou seja, a arena do espaço-tempo.

Nós agora iremos tratar de uma outra escolha de representação de natureza diferente.  É ela que constitui a base do que poderíamos chamar a desconstrução do real.

Em um primeiro momento, tratou-se da escolha de um conveniente sistema de coordenadas espaciais. Depois, com a unificação espaço-tempo, coordenadas espaciais e temporal.

Até aqui, considerávamos o espaço-tempo absoluto, em substituição ao espaço absoluto e tempo absoluto.

Com a teoria  da relatividade geral (RG) foi a própria estrutura do espaço-tempo que teve que ser modificada. Passou-se a imaginar que a geometria do espaço-tempo contenha toda a informação da interação gravitacional.

Criou-se um paradigma: a estrutura métrica do espaço-tempo é devida à universalidade da gravitação e somente esta interação determina a geometria do mundo.

Entretanto, a estrutura métrica do espaço-tempo pode ser alterada em outras representações, seja substituindo forças arbitrárias onde escolhemos descrever esse processo via modificação da geometria, seja na questão de transformação de uma dada teoria por outra. Veremos dois exemplos a seguir, a teoria da relatividade métrica (TRM) e a descrição da geometria efetiva eletromagnética (não se trata da teoria unificada).

Teoria da Relatividade Métrica

Na Física, afirma-se que um corpo é livre se sobre ele não existem forças externas atuando. Nesse caso, seu movimento inercial é descrito por caminhos no espaço-tempo chamados geodésicas. Ou seja, a geodésica é a trajetória de um corpo sem que sobre ele esteja atuando uma força externa. Note que mesmo quando observamos em nosso cotidiano um corpo em repouso (em uma determinada referência espacial) ele segue um caminho (uma geodésica) no espaço-tempo quadridimensional:  a continuidade temporal o exige.

Reconhecemos três leis físicas fundamentais que descrevem completamente todos os movimentos dos corpos envolvendo teorias da relatividade, que se distinguem pelos qualificativos especial, geral e métrica.

• Cada coisa, cada observador, possui um tempo próprio distinto dos demais. Essa propriedade permite organizar uma estrutura métrica quadridimensional espaço-tempo estática, absoluta e única, chamada geometria de Minkowski;
• A ação de uma força gravitacional, por ser ela universal, pode ser eliminada através da modificação da arena onde o fenômeno se passa, a geometria de Minkowski, gerando uma nova geometria que controla dinamicamente as distâncias no espaço e no tempo;
• A prática de estender o método de eliminação da força gravitacional para qualquer outro tipo de força pode ser realizada através da construção de uma nova geometria específica, uma para cada corpo.

Esses três momentos merecem comentários adicionais.

Relatividade Especial

Uma das consequências mais notáveis da teoria da Relatividade Especial (H. Poincaré e A. Einstein, 1904) foi a substituição de um único tempo comum a todos os corpos por uma infinidade de tempos próprios, um para cada corpo ou observador.  Dessa forma, a tradicional geometria euclidiana usada no cotidiano e dominante na física clássica foi substituída por uma outra geometria na qual além das três dimensões do espaço se acrescenta uma dimensão temporal.  Nessa descrição cada observador passa a ter um seu tempo próprio e a noção de simultaneidade passa a depender de seu estado de movimento. Essa transformação de um tempo único universal para uma miríade de tempos, um para cada observador, retirou de cena o tempo absoluto newtoniano.

Relatividade Geral

Em um momento posterior, na década de 1920, o aparecimento da teoria da Relatividade Geral (A. Einstein, 1915), que nada mais é do que uma teoria da gravitação associada à modificação da geometria induzida pela distribuição de matéria e energia, retirou o caráter imutável, rígido, estático da estrutura minkowskiana.

A geometria experimentada por um corpo, aquilo que caracteriza distâncias no espaço e no tempo, adquiriu assim uma estrutura variável, dependente da interação com outros corpos, ou melhor, dependente da quantidade de matéria e energia presente.  A universalidade da gravitação – isto é, o fato de que todos os corpos sentem a ação da força gravitacional – foi responsável pela modificação da geometria do mundo, pelo reconhecimento de que toda matéria, tudo que existe, está imerso em uma única e global estrutura geométrica. O caráter universal da interação gravitacional fixa uma única geometria onde tudo-que-existe está mergulhado nessa totalidade espaço-tempo.

Desse modo, a ação da força gravitacional é identificada à transformação da geometria por onde o corpo físico se movimenta. Nesse procedimento a gravitação é formalmente eliminada, reaparecendo travestida sob a forma de modificação da geometria. Ou seja, o fenômeno gravitacional passa a ser interpretado como se não houvesse a força gravitacional: o movimento dos corpos materiais é descrito como se eles seguissem caminhos livres mas em um espaço-tempo de geometria variável. Esses caminhos onde nenhuma força atua são as geodésicas.  Assim, pode-se afirmar que a força gravitacional não existe strictu sensu pois foi substituída pela modificação universal (sentida por todos os corpos) da geometria onde o corpo se encontra.

O caminho, livre de qualquer força, é identificado com as curvas geodésicas definidas pela geometria. Nesse contexto, pode-se afirmar que um corpo é livre se sobre ele atuam somente o que tradicionalmente chamamos forças gravitacionais. 

Recentemente (M. Novello e E. Bittencourt, 2015)  esse método de eliminação da força gravitacional por uma geometrização especial foi generalizado para poder ser aplicado a todos os tipos de forças na teoria da relatividade métrica.

Relatividade Métrica

Um corpo atuado por qualquer força (não gravitacional) não é livre. Tal descrição permitiria caracterizar de um modo absoluto o que chamaríamos “liberdade na Física”.  Pois bem, muito recentemente descobriu-se que esse não é o caso e que a noção de “corpo livre” depende igualmente da estrutura métrica do espaço onde esse corpo é descrito. Dito de outro modo: um corpo submetido a uma força de qualquer tipo em um dado espaço-tempo pode ser descrito, de modo equivalente, como se estivesse livre de qualquer força desde que ele passe a ser descrito como se estivesse mergulhado em uma outra geometria específica, dependente das propriedades de movimento do próprio corpo.  Isso significa que cada corpo possui uma “sua” geometria na qual o efeito da força externa que sobre ele atua é substituído pelas propriedades da geometria onde o corpo passa a ser descrito.

Ainda que à primeira vista se trate do mesmo procedimento realizado na teoria da relatividade geral há, no entanto, uma diferença notável: no caso gravitacional essa mudança da geometria é universal ou seja independe de qualquer característica do corpo em questão; enquanto no caso de um corpo qualquer atuado por uma força não gravitacional a alteração das distâncias espaço-temporais dependem da particular dinâmica do corpo. Mesmo não tendo um caráter universal, devemos reconhecer que esse procedimento produz um resultado notável: a substituição dos efeitos da aceleração de um corpo atuado por força de qualquer natureza, por um caminho geodésico em  um espaço-tempo de geometria modificada. O corpo, desprovido de aceleração nessa geometria efetiva, é então considerado como um corpo livre.

Recentemente, esse mecanismo de transformar a descrição de processos dinâmicos exercido por forças de qualquer natureza por alterações na geometria por onde o corpo se movimenta mostrou ser bastante geral e pode ser aplicado a todo tipo de força e a qualquer corpo físico.  Isso leva a um modo novo de descrever processos dinâmicos e que consiste naquilo que chamamos teoria da Relatividade Métrica.

Desconstruindo o espaço-tempo

Vimos que a evolução da estrutura da geometria do espaço-tempo desde o começo do século XX até os dias de hoje pode ser descrita por três momentos principais de síntese, a saber:

• A Relatividade Especial, no começo do século XX, se fundamentou sobre o princípio de que cada observador possui um tempo próprio e se movimenta em um espaço-tempo único possuindo uma geometria estática, sem curvatura e absoluta;
• A Relatividade Geral na segunda década daquele século alterou essa geometria mantendo sua universalidade, mas tornando-a variável;
• A Relatividade Métrica no século XXI, se baseia no princípio de que cada observador, sobre o qual atuam diferentes forças, institui sua própria geometria onde as forças que atuam sobre ele são formalmente eliminadas. Como a geometria resultante (aquela onde o corpo está livre de qualquer ação e se movimenta ao longo de uma geodésica nessa geometria associada) depende do movimento, concluímos que cada corpo possui uma sua geometria particular na qual ele é um corpo livre, isento de qualquer ação externa. Essa eliminação da força pela caracterização de uma geometria especifica para cada corpo é uma simples questão de escolha de representação. Adquire-se então uma novidade inesperada: a liberdade dos corpos na física depende da representação escolhida.  Assim como na sociedade onde a liberdade é relativa, também na ciência Física, contrariamente ao senso comum, a liberdade das coisas não tem caráter absoluto.

Vamos dedicar um pouco mais a descrever alguns detalhes a essa questão.

Liberdade absoluta, liberdade relativa
(resumo de uma palestra em 14 novembro 2014 na USP)

Preâmbulo

Os filósofos falam da liberdade. Os juristas também, assim como os psicólogos. Conhecemos na literatura como alguns poetas a tratam. Seja com Camus na filosofia do absurdo ou no existencialismo de Sartre; ou nos textos nietzschianos do escravo que oculta de seu senhor erros cometidos, reconhecemos  como é complexo e cheio de invisíveis astúcias as expressões e interpretações produzidas pelos romancistas sobre a liberdade individual e coletiva que a humanidade ao longo de sua história dispõe em diferentes graus de autonomia.

No mundo das coisas aceitamos que um corpo é livre se nenhuma força atua sobre ele. Existe uma tendência, implícita nos pensadores das áreas humanas a acreditar (talvez devido à uma suposta condição de inferioridade em relação à ciência) que na física esse conceito de liberdade possui um conteúdo especial como se estivesse estruturado em um modo absoluto. Ao tratarmos da liberdade no território da ciência espera-se produzir manifestações mais sólidas e completas e, consequentemente, mais seguras. É assim que os cientistas a apresentam.

Essa noção de liberdade na física se construiu de modo especial mas histórico, semelhantemente como a elaboraram ao longo dos tempos filósofos, psicólogos, juristas, sociólogos. Com uma substancial diferença: há um consenso de que na sociedade humana a liberdade é relativa.  Entretanto, ao ser transportado esse conceito para a ciência, aparece a expectativa de que ele perca esse caráter social e relativo, adquirindo uma versão absoluta. Isso é consequência direta do status da atividade cientifica, do lugar especial que ocupa no imaginário moderno pois entende-se que a ciência fala do território da verdade e não da opinião; não fala da política, não fala do homem, mas sim “da natureza”.

E no entanto, a situação é um pouco menos simplista e a propriedade de produzir uma liberdade absoluta atribuída à física está longe de ser verdadeira. Como é isso possível é o que iremos descrever.

Uma geometria no mundo

Sabemos, há muito tempo, como medir distâncias. Produzimos uma geometria euclideana. Pensávamos que essa geometria fosse única, dada pela intuição e identificada à experiência de cada um de nós. Fomos alertados no inicio do século XX  pelos homens da ciência da física e da matemática que essa geometria não descreve a totalidade de nossa observações. É preciso ir além. E fomos. Tomando como ponto de apoio as reflexões de vários matemáticos como Gauss, Lobachewski e Riemann, produziu-se uma geometria inusitada e que identificamos pelo nome de um desses cientistas: Minkowski.

Até a primeira década daquele século a descrição do palco onde os fenômenos físicos aconteciam identificava-se com um espaço tridimensional no qual o conceito de distância era controlado pela geometria euclidiana. Com a construção da teoria da Relatividade Especial, elaborada por Poincaré, Lorentz, Fitzgerald, Minkowski, Einstein e outros, esse cenário foi alterado. Passou-se daquela estrutura rígida e única a três dimensões para uma estrutura rígida e única a quatro dimensões com a introdução de uma nova variável, o tempo.

Uma das consequências desse procedimento foi a substituição de um único tempo comum a todos os corpos por uma infinidade de tempos próprios, um para cada corpo ou observador.  Como consequência, a geometria euclidiana foi substituída pela geometria de Minkowski, uma estrutura formal particular das geometrias possíveis construídas por Riemann (citar/foto da tese). Cada observador tem assim o seu tempo próprio e a noção de simultaneidade passou a depender do observador. Essa passagem de um só tempo para uma miríade de tempos relativos a cada observador deslocou de cena o tempo absoluto newtoniano.

Em um momento posterior, na segunda década do século XX, o aparecimento de uma nova teoria da gravitação associada à modificação da geometria riemanniana pela matéria e energia, retirou o caráter imutável, rígido, estático da estrutura minkowskiana passando a considerar o espaço-tempo como possuindo uma geometria variável, dependente da quantidade de matéria e energia existente em uma dada região.

A universalidade da gravitação foi então responsável pela modificação da geometria do mundo, afirmando que toda matéria, todo observador, está imerso em uma única e global estrutura geométrica, variável, possuindo uma dinâmica controlada pela matéria. A característica importante a reter aqui é precisamente a preservação dessa univocidade, ou seja, existe somente uma geometria no mundo. O caráter universal da interação gravitacional fixa a geometria onde tudo-que-existe está mergulhado, ou seja, a totalidade espaço-tempo.

Há uma outra propriedade notável na teoria da Relatividade Geral que requer um comentário especial. Trata-se da eliminação da força gravitacional. Mais precisamente, a força gravitacional é substituída pela alteração na geometria do espaço-tempo. Na física pré-relativista newtoniana, todo corpo submetido à ação gravitacional adquire uma aceleração. Na moderna teoria da gravitação, o fenômeno da aceleração resultante da interação gravitacional é substituído por modificações na geometria por onde o corpo se movimenta, de tal modo que na nova configuração métrica o corpo, qualquer corpo, pode ser descrito como livre de ação externa.

Ou seja, nessa nova estrutura métrica o corpo que interage gravitacionalmente é entendido como livre. A gravitação deixa de ser uma força conforme era estabelecido no esquema newtoniano e passa a ter o controle da variável geometria do mundo. Nesse espaço-tempo de geometria cambiante, o corpo percorre uma trajetória – chamada geodésica – que caracteriza um corpo livre de qualquer força. Tudo se passa como se a interação gravitacional alterando a geometria deixa o corpo livre dessa força, mas lhe indica o caminho a percorrer. Isso só é possível porque todos os corpos reagem de forma equivalente à ação gravitacional. Assim, todos os corpos se encontram embebidos em uma mesma geometria. É precisamente essa universalidade que torna possível a identificação dos efeitos gravitacionais sobre os corpos como alterações efetivas na métrica do espaço-tempo, afetando as distâncias espaço-temporais.

Depois da grande revolução einsteiniana da relatividade geral e do reconhecimento de que a universalidade dos processos gravitacionais implica em modificação da geometria do mundo, concluiu-se que a física havia consagrado uma nova descrição absoluta, posto que qualquer outra força de caráter não-gravitacional exerce uma ação sobre o corpo que o desvia da geodésica. Ou seja, parecia que se poderia afirmar que um corpo é livre se sobre ele atuam somente forças gravitacionais (pois estas são representadas por caminhos de corpos livres, as geodésicas, em um espaço-tempo de geometria variável).  Por outro lado, um corpo atuado por outras forças não é livre. Tal descrição permitiria caracterizar de um modo absoluto o que chamaríamos “liberdade na física”.  Pois bem, muito recentemente descobriu-se que esse não é o caso, como veremos.

Corpo livre

Podemos aceitar, provisoriamente, a definição tradicional de que um corpo deve ser considerado livre se não existe nenhum agente externo, nenhuma força atuando sobre ele. Sabemos que um corpo pode estar em movimento e no entanto ser livre. Ou seja, a liberdade não é sinônimo de estado estático. Atribuímos um nome a essa propriedade da matéria: inércia. Desde a antiguidade sabemos que um corpo isento de forças segue uma trajetória reta. Ou melhor, segundo os matemáticos, segue uma geodésica – que é o termo que corresponde ao movimento livre de forças. A geodésica é o caminho natural por onde seguem os corpos livres.

Na física moderna relativista o palco onde ocorrem todos os fenômenos está determinado pela estrutura espaço-tempo: um conjunto infinito de pontos quadri-dimensionais no qual três valores são atribuídos ao que chamamos espaço e um quarto número é associado ao tempo. Nesse palco 4-dimensional o caminho natural de um corpo, livre de qualquer força é uma geodésica e corresponde ao menor caminho para ir de um ponto a outro desse espaço-tempo.

A geodésica, conhecida dos matemáticos, constitui uma curva especial: um corpo que a percorre não possui aceleração. Podemos então afirmar que um corpo deve ser considerado livre (de forças externas) se, ao seguir uma trajetória, ele se movimenta sobre uma curva especial – a geodésica –na qual sua velocidade é constante. Isto é, todo caminho identificado a uma geodésica em um dado espaço, não possui aceleração. Inversamente, todo corpo que não possui aceleração se movimenta sobre uma curva geodésica.

Embora o conceito de geodésica seja mais amplo, eu limitarei sua análise aqui àquilo que os matemáticos chamam espaços métricos, isto é, aqueles nos quais a noção de distância, através da criação de uma métrica, foi estabelecida.  Assim, cada estrutura geométrica, cada espaço métrico (isto é, um espaço contendo pontos geométricos e ao qual se atribuiu uma métrica capaz de definir nesse espaço uma distância) possui caminhos especiais – as geodésicas – que minimizam a distância entre dois pontos. Ou seja, para ir de um lugar – digamos, do ponto A – para ir a um outro lugar – digamos o ponto E — de tal modo que essa distância entre A e E seja mínima, ele deverá seguir uma geodésica. Esse conceito vale para qualquer tipo de espaço. Por exemplo, para ir de um ponto de uma rua a outro ponto, reconhecemos intuitivamente qual o menor caminho: uma reta, caso esse caminho seja acessível. Para ir de um ponto da Terra (ou sobre um globo terrestre que represente nosso planeta) a um outro ponto, sabemos que devemos seguir um certo caminho curvo que consiste no caminho “mais reto” possível, ou seja uma geodésica. Nessa segunda situação a linha reta convencional não é accessível devido à curvatura intrínseca do globo terrestre.

Antecedentes da Relatividade Geral: o princípio de d´Alembert

Os historiadores da ciência, baseados em relatos de físicos, com frequência comentam seu espanto com o reconhecimento de que Einstein teria elaborado a relatividade geral sem se apoiar em nenhuma teoria precedente. Embora seja correto afirmar que a proposta de geometrização da força gravitacional tenha sido desenvolvida praticamente por um só personagem, houve vários indícios aqui e ali que contestam aquela versão isolada e a-histórica na elaboração da relatividade geral. Com efeito, essa imagem parece não corresponder ao que efetivamente aconteceu. Havia um fio de pensamento, uma sequência de ideias subjacentes e que podemos remontar a vários cientistas, como por exemplo, o matemático Riemann em sua tese de habilitação conjecturou sobre a relação entre a geometria e as propriedades da matéria; e, de modo implícito nas ideias do matemático francês Jean d´Alembert (século 18).

O princípio de d´Alembert foi usado na mecânica newtoniana para transformar formalmente a análise do movimento de um corpo acelerado por diversos e diferentes tipos de forças, em um problema equivalente em repouso. Isto é, somando-se todas as forças que atuam sobre um corpo incluindo as forças de inércia, chega-se ao resultado que a soma total é zero. Isso equivale então, formalmente, a transformar um problema dinâmico (corpo em movimento acelerado por forças externas) em um problema estático onde o corpo em questão não é atuado por nenhuma força.

Na interpretação de Einstein das forças gravitacionais uma análise semelhante foi empreendida. Na teoria da relatividade geral argumenta-se que as consequências da ação da gravitação sobre um corpo podem ser substituídas ou melhor essa ação pode ser eliminada através da modificação da geometria do espaço-tempo subjacente a esse corpo. Isto é, a alteração da geometria permite descrever o movimento de qualquer corpo em um campo de forças gravitacional como se essa força tivesse sido eliminada. Em verdade ela não foi eliminada mas sim, como no princípio de d´Alembert, gerou-se formalmente uma estrutura que permite interpretar o movimento dos corpos como não-acelerados. Esses são os caminhos que um corpo segue em uma estrutura quadri-dimensional espaço-tempo livre de qualquer força, as geodésicas; o espaço-tempo ganha uma métrica que estabelece uma geometria riemanniana.  A métrica é o resquício da força gravitacional e tem a função de substituir as propriedades tradicionalmente atribuídos àquela força. Ou seja, a teoria da relatividade geral mostrou que ao invés de pensarmos a força gravitacional como exercendo uma ação sobre um corpo ela pode ser eliminada da descrição e substituída por uma alteração na geometria.

Na teoria da relatividade geral, Einstein deu um passo notável ao sugerir que o princípio de d’Alembert poderia adquirir uma nova e inesperada formulação. Poder-se-ia eliminar a força gravitacional se ao invés de descrever a trajetória de um corpo descrita convencionalmente no espaço-tempo plano, sem curvatura, o espaço-tempo de Minkowski, a descrevêssemos como uma geodésica  em um espaço curvo, variável, característico de cada configuração do campo gravitacional.

O fato de que a utilização do princípio de d´Alembert se limita, na visão de Einstein, ao campo gravitacional, repousa sobre o princípio de equivalência que garante a universalidade da experiência de Galileu, segundo a qual os corpos – independentemente de suas configurações e formas e substâncias, adquirem a mesma aceleração em um campo gravitacional. Graças a essa universalidade da aceleração comum a todos os corpos foi possível substituir formalmente os processos gravitacionais como alterações na geometria do espaço-tempo.

Em síntese, a aceleração que a força gravitacional exerce sobre todo corpo pode ser descrita como se sobre esse corpo não se exercesse nenhuma força, mas sim o espaço-tempo, o território por onde o corpo se movimenta, fosse dotado de uma geometria distinta, possuindo uma curvatura que lhe concede caminhos (as geodésicas) especiais nessa geometria.  Esses caminhos são utilizados por qualquer corpo, independente da sua massa e da substância com o qual ele é formado. Isso vale também para corpos sem massa, como os grãos de luz, os fótons.

Ou seja, ao invés de pensar a gravitação como uma força atuando sobre um dado corpo e modificando sua trajetória no mundo, a hipótese feita na relatividade geral propõe a substituição dessa força por uma modificação na geometria do espaço-tempo que é o que restou da ideia newtoniana de força gravitacional.  Consequentemente o movimento do corpo é descrito como se sobre ele não atuasse nenhuma força e, na geometria alterada, ele se deixaria levar por sua inércia: o corpo é considerado livre.

Aparece a questão: uma situação semelhante pode ocorrer para corpos submetidos a outras forças? Ou seja, a caracterização da liberdade ou não de um corpo é universal? Isso é, pode um corpo ser “relativamente livre” ou devemos pensar a liberdade como absoluta? No caso da gravitação, devido à sua universalidade e às propriedades especiais típicas da ação gravitacional, sabemos que a liberdade pode ser entendida como absoluta. Mas e quanto às outras forças que podem atuar sobre um corpo?  Aceita-se que somente a gravitação com sua universalidade permite a substituição da força por alterações na geometria. No entanto, um procedimento semelhante pode ser usado no caso de forças de origem não-gravitacional. É razoável esperar que no caso de forças não-gravitacional a característica dessa geometria seja menos universal.  Para entender como isso pode ocorrer é conveniente e didático fazermos um breve desvio e considerar um resultado notável referente à eletrodinâmica dos corpos em movimento.

Entra em cena Gordon e o fenômeno dos caminhos da luz no interior de corpos dielétricos em movimento

Certas substâncias que não são condutoras de eletricidade podem ser polarizadas graças a um campo elétrico a que são submetidas. São então chamadas de material dielétrico. A propagação da luz nesses meios dielétricos é em geral caracterizada por uma constante, chamada permissividade dielétrica, que no vácuo tem o valor unitário. No vácuo, os grãos-de-luz chamados fótons, possuem a mesma velocidade independentemente de qual seja o estado de movimento ou repouso do observador. No entanto em um meio dielétrico essa velocidade varia em função dessa permissividade. Dito de outro modo, nesse meio a luz adquire uma aceleração. Um tal fato não contradiz a teoria da relatividade especial que afirma a constância da velocidade da luz no vácuo, fora de qualquer substância material.

O físico W. Gordon em 1923 produziu uma descrição particularmente eficiente e elegante desse processo de aceleração no interior de dielétricos em movimento. Ele se perguntou se seria possível aplicar o método utilizado por Einstein para substituir a força gravitacional através da alteração de réguas e relógios (ou seja, os aparelhos com quais se mede distâncias no espaço e no tempo) para descrever a propagação da luz no meio dielétrico de tal modo a associar um espaço-tempo curvo ao caminho da luz e eliminar assim sua aceleração.

Isso é realmente possível e Gordon descreveu as propriedades dessa métrica efetiva que substitui o efeito de aceleração do fóton no meio dielétrico por uma equivalente alteração da geometria. Dessa forma o fóton, nessa geometria, segue uma geodésica; sua aceleração se esconde na expressão variável da geometria que o fóton reconhece como a do espaço-tempo onde ele se propaga.

Embora à primeira vista se trata do mesmo procedimento realizado na teoria da relatividade geral há uma diferença notável: no caso gravitacional essa mudança da geometria é universal ou seja independe de qualquer característica do corpo em questão; enquanto no caso do fóton no interior de um meio dielétrico em movimento, a alteração das distâncias espaço-temporais só seriam experimentadas pela luz.

Mesmo não tendo um caráter universal, devemos reconhecer que Gordon produziu um resultado notável: a substituição dos efeitos da aceleração do fóton em um meio dielétrico por um caminho geodésico em um espaço-tempo curvo. O fóton, desprovido de aceleração nessa geometria efetiva, deve ser considerado como um corpo livre.

Generalização do princípio de d´Alembert: teoria da Relatividade Métrica

Na física, estamos acostumados a identificar a ordem do mundo através de representações que requerem um pano-de-fundo ou cenário que contém os fatos; um recipiente, um abrigo, um lugar, um território especificado no espaço e no tempo. Na visão newtoniana que dominou até o iní cio do século XX a descrição da física, podíamos recorrer a uma estrutura absoluta e universal que chamou-se espaço e tempo absolutos.  Fomos informados que na primeira década do século XX uma mudança nesses absolutos se estabeleceu e organizou-se uma nova ordem estruturando um espaço-tempo absoluto mas solidário. Os dois infinitos absolutos fundiram-se em um só.

A geometrização empreendida na Relatividade Geral é entendida como única e universal. O mundo possui assim uma geometria em uma dada situação que representa a ação gravitacional. A interação entre corpos passou a ser descrita não mais como uma força entre os corpos mas sim como uma ação indireta através da modificação  desse tecido substancial que se entende hoje por espaço-tempo. O cenário, e não os atores, é alvo de ações constringentes. Os atores sofrem a ação do palco pois são obrigados a se movimentarem de um modo especifico devido às configurações que a modificação da geometria (a ação gravitacional) produz. Isso nós aprendemos da física do século XX e produziu uma alteração profunda na representação dos fenômenos.

No entanto, muito da ordem anterior foi preservada. Dentre os aspectos mantidos, o mais importante — para uma certa visão externa ao mundo da física, aquela que estamos querendo identificar como aspectos da cultura a serem roubados da ciência para serem usados em outras representações, em outras áreas de diferentes saberes – consiste na univocidade da geometria do mundo.

Embora diferentes ações gravitacionais produzam diferentes geometrias, para cada ação existe uma única geometria que é percebida universalmente. Ou seja, tratamos em cada fenômeno de uma só representação do espaço-tempo que é   considerada assim a arena comum. Pois bem, é precisamente essa univocidade que está sendo posta em jogo, é ela que está sendo questionada e é ela que talvez esconda uma mudança inesperada na descrição do mundo. É possível que sejamos levados a repensar a necessidade desse mundo comum que tratamos com intimidade e sobre o qual convencionamos que é onde se desenrolam os fenômenos. Estamos assim preparados para compreender a ideia da multiplicidade de geometrias, uma para cada observador.

A organização dos fenômenos a partir de um cenário identificado com um espaço-tempo único, comum a tudo-que-existe, foi uma construção que teve muito sucesso na ciência e mesmo além dela. Essa ideia serviu para poder distinguir claramente as substâncias, os corpos materiais e suas interações do território onde os processos físicos efetivamente ocorrem. A totalidade de nossa descrição dos fenômenos no mundo é pensada em um cenário único, usamos um só palco para organizar toda a trama que acontece na natureza.

Essa descrição unificada agrada os físicos pois ela faz parte do programa estabelecido apriori de reduzir sempre e cada vez mais, as quantidades necessárias com as quais se pode produzir uma explicação científica. Ela é típica da ordem gerada a partir do uso do processo mental de simplificação chamado navalha de Occam.

É, no entanto, possível produzir uma descrição dos fenômenos de outro modo, pois não há nenhuma razão formal que a impeça. A não aceitação da existência de uma única estrutura espaço-tempo não entra em choque com nenhuma hipótese mais fundamental.  A escolha de uma interpretação dos fenômenos a partir da hipótese de que eles convivem em uma mesma estrutura, em um só palco, em um só espaço-tempo é somente uma feliz e bem-sucedida hipótese de trabalho. Significaria isso que estejamos próximos do momento em que o monismo que tem servido para adquirir controle e produzir utensílios, favorecendo a técnica em detrimento da contemplação, está saindo de cena? E se isso é verdade, qual imagem mental desse novo modo de descrever o universo podemos construir?  Vamos deixar essa questão em suspenso e voltar a ela em outro lugar. Continuemos nossa análise da questão da liberdade dos corpos. Para sustentar essa análise e dar sentido a essa aparente violação de um paradigma vamos dedicar nossa atenção ao que chamamos Relatividade Métrica. 

Uma geometria no mundo?

Os comentários anteriores enfatizaram a relação da geometria do espaço-tempo com os processos de interação gravitacional. Vamos agora tratar de uma questão que alarga o alcance da questão geométrica proposta pela Relatividade Geral baseada em diversos artigos científicos que estão produzindo reformulações de antigas questões que parece serem melhor compreendidas fora da cena cientifica e que pode ser sintetizada na sentença provocadora e inesperada: “o mundo perdeu sua geometria única e diluiu-se em infinitas formas métricas”.  Como entender essa afirmação? Vejamos.

A física trata de situações várias dentre as quais uma típica consiste em descrever a ação de forças externas sobre um corpo qualquer. Desse modo, com essa descrição separou-se o mundo em “um corpo A” e “o resto” ou “os outros corpos”. O caminho do corpo A é controlado e/ou alterado pelos outros corpos. Dizemos que os outros corpos exercem uma força, uma ação direta ou indireta sobre A. É verdade que nenhum corpo é isolado. O mundo consiste em um processo ininterrupto de interação. A ciência tem procurado como objetivo maior unificar esses diferentes processos de interação. Diferentes modos apresentam diferentes variáveis, com maior ou menor grau de complexidade. Podemos usar o poder de síntese da matemática para reduzir esse número. A questão que se coloca então é: quão longe podemos ir nessa simplificação?  Quanto podemos reduzir a ação externa sobre um corpo? E, afinal, seria possível encontrar um modo de representação na física que reduziria totalmente essa ação externa, substituindo-a por uma estrutura menos “externa”, podendo incorporá-la à própria constituição do caminho que um corpo qualquer é levado a seguir? Dito de outro modo: posso eliminar completamente a ação dos outros corpos sobre um dado corpo? É possível eliminar a ação dos outros sobre meu caminho?

Antes de responder, antecipa-se uma outra questão: um tal solipsismo seria aceitável? Consistiria isso em uma representação da interação dos corpos no mundo? Haveria ainda uma estrutura fundamental? Uma força qualquer atuando sobre um corpo pode ser representada como uma ação que, reconhecendo “o corpo e suas circunstâncias” pode abandonar a visão tradicional de força ou, em uma linguagem moderna, todo processo de interação?

Curiosa e inesperadamente a resposta é sim, essa simplificação é possível. O método? Semelhante ao que a física clássica já inventara; que a Relatividade Geral de Einstein usou e Gordon estendeu através da alteração da geometria no interior de meios dielétricos. O resultado dessa análise é que é possível reduzir a ação de todos os outros corpos – o “resto do universo” – modificando as propriedades que sempre estiveram associadas à geometria do espaço-tempo. Ou seja, as forças externas que um corpo sofre podem ser igualmente representadas por uma alteração na geometria; a alteração da geometria passa a ser sinônimo da contabilização dos efeitos externos, no que chamamos Teoria da Relatividade Métrica

Para que isso seja possível e que a força externa desapareça da descrição do mundo para cada corpo (e para todos os corpos) devemos descrever o caminho do corpo, sua trajetória, como livre. Ou seja, deve-se alterar a geometria onde o corpo se move, permitindo a descrição de seu movimento como curvas geodésicas em uma geometria modificada. É precisamente essa propriedade que caracteriza a nova geometria experimentada por esse corpo. Ela é construída com propriedades do corpo (sua velocidade) e da força externa (sua aceleração).

A Relatividade Especial, na primeira década do século passado, permitiu passar da noção de que devemos caracterizar a realidade dos fenômenos abandonando a hipótese de um só tempo universal para uma infinidade de tempos próprios, um para cada observador. A relatividade métrica está produzindo a ideia de que se deve passar da geometria única para uma multiplicidade de geometrias, uma para cada observador.

Conclusão

A Relatividade Especial se fundamenta sobre o princípio de que cada observador tem um tempo próprio e se movimenta em um espaço-tempo único possuindo uma geometria comum. A Relatividade Métrica se baseia no princípio de que cada observador, sobre o qual atuam diferentes forças, institui sua própria geometria onde as forças que atuam sobre ele são formalmente eliminadas. Como a geometria resultante (aquela onde o corpo está livre de qualquer ação e se movimenta ao longo de uma geodésica nessa geometria associada) depende do movimento, concluímos que cada corpo instaura uma sua geometria particular na qual ele é um corpo livre, isento de qualquer ação externa.

O abandono de um tempo único, proposto pela teoria da Relatividade Especial constituiu uma desconstrução. O abandono da geometria única é uma outra forma de desconstrução gerada pela teoria da Relatividade Métrica.

A teoria da multiplicidade geométrica provoca uma transformação significativa e bastante distinta da convencional na descrição dos fenômenos. A propriedade notável está contida na afirmação de que podemos descrever o caminho de um corpo quer considerando a ação de forças externas em um cenário de espaço-tempo comum ou considerar que esse espaço-tempo possui alterações individualizadas de sua geometria. Nesse segundo caso, um corpo se movimenta através de caminhos especiais, as geodésicas dessa geometria, livre de força externa. Ambas as descrições são corretas. Trata-se somente de uma escolha de representação. Tanto um quanto o outro modo de representar o movimento de um corpo possui vantagens e desvantagens. Não estou interessado aqui nessa contabilidade, mas somente em exibir essa nova descrição, que leva a uma extensão do conceito de liberdade.

Mudar a geometria do mundo para um dado observador equivale a descrever seu caminho como isento de qualquer forma de interação; caminho da geodésica, aqueles que são naturalmente privilegiados pela geometria.  O observador se vê mergulhado em “sua” geometria, de modo análogo, mas distinto, do observador na relatividade especial quando adquiriu o status de ter “seu próprio tempo”. Não se trata, a não ser aparentemente, de um solipsismo, pois a base dessa alteração da geometria não depende somente do observador, mas também de seu exterior, o resto-do-universo. Essa estrutura única, jogada no mundo como ele mesmo, como sendo do-mundo, desmorona,  descontrói-se, deixando de ser-do-mundo para vir a constituir uma particular propriedade de cada corpo.

Assim organiza-se a equivalência entre dois modos de descrever os movimentos dos corpos. Podemos dizer:

Existem forças atuando sobre cada corpo que orientam seu caminho em uma estrutura única, comum e universal que chamamos espaço-tempo;

Ou, equivalentemente,

Todo corpo segue caminhos sempre livres em seu particular espaço-tempo ao qual é atribuída uma geometria.

A modificação da geometria substitui a ação da força que caracteriza um agente externo. A descrição dos processos físicos em uma unidade formal que se chamou espaço-tempo é uma convenção útil. Nada mais do que isso. Sua realidade provém dessa aceitação.

Na representação individualista, não temos controle sobre as propriedades especificas em cada caso dessa geometria, pois elas dependem de fatores externos; por razão semelhante não temos controle sobre as propriedades específicas das forças que agem sobre cada corpo na versão unificada, pois elas dependem igualmente de fatores externos.

A criação de um mundo único, uma estrutura única que contém tudo-que-existe, faz parte da visão moderna da ciência. Ela é útil e eficiente. Nesse texto pretendi retirar o peso de que isso seja uma verdade absoluta, quando nada mais é do que uma convenção. Do mesmo modo para responder à pergunta se um dado corpo está livre (de ações externas) devemos antes fixar a qual geometria do cenário espaço-tempo queremos nos referir. No caso das forças gravitacionais essa alteração da geometria é universal, a mesma para todos os corpos; no caso de qualquer outra força, essa geometria é particular, individualiza a força e o corpo. Em ambos os casos a escolha de se um corpo está livre ou não depende do modo pelo qual ele e seu contexto geométrico é descrito. O que leva a afirmar que na física, assim como nas ciências humanas, o conceito de liberdade não possui caráter absoluto, ou seja, toda liberdade é relativa.

Do que vimos, concluímos que a geometria do espaço-tempo onde são descritos os fenômenos no mundo depende da escolha de representação. Ou seja, a estrutura fundamental da qual nos servimos para representar a arena dos processos físicos, os fenômenos do mundo, se desfaz como uma estrutura única, sólida, universal. Passa a ser dependente do modo pelo qual qualquer observador faz uma escolha particular para representar os fenômenos. Dilui-se a rigidez do espaço e do tempo, instaura-se a desconstrução do espaço-tempo único, comum.

 O Cosmos solidário

No livro La solidarité, enquete sur um príncipe juridique, Alain Supiot coordena um exame cuidadoso da evolução do conceito solidariedade. Esse exame se estende desde as longínquas origens jurídicas do termo até questões atuais em diversas áreas, como a biologia, a sociologia, a política, e em diferentes épocas geográficas e históricas.

Neste livro André Pichot apresenta diversos aspectos da solidariedade na biologia e compara com a utilização da sociologia num quadro de analogia darwiniana.

Uma ausência notável, a relação da solidariedade com a ciência da física. Curiosamente, essa ausência é entendida como natural, pois solidariedade é um conceito que não seria aplicável ao universo, mas somente à espécie animal.

No entanto, a cosmologia permite a aplicação desse conceito, solidariedade, ao universo. Mais do que isso, ele pode contrabalançar o papel autoritário e arrogante de uma proposta que pretende dar ao universo um sentido de caráter eminentemente antropomórfico através da utilização do princípio antrópico.

Neste caso, solidariedade pode ser entendido como compatibilidade, coerência no sentido da matemática e da física. Vejamos o que aparece no Manifesto Cósmico e que apontamos atrás no capitulo 1.

Até muito pouco tempo a microfísica e, de modo mais amplo, a física terrestre eram pensadas fora do contexto cósmico. Elas pareciam não necessitar de explicação ulterior, eram tratadas como sistemas autorreferentes, sem admitir qualquer forma de análise extrínseca para constituir uma razão auto-consistente. No entanto, nas últimas décadas a cosmologia invadiu abruptamente esse domínio tranquilo do pensamento positivista dominante e destruiu a paz racional daqueles que acreditam que a Terra, os homens, possuem um papel especial no universo.

Essa interferência cósmica sobre a física local não deve ser entendida como a substituição de uma razão absoluta por outra razão absoluta. Não se trata de trocar o absolutismo associado ao caráter universal da física local pelo absolutismo de uma física global. A questão é um pouco mais complexa. O matemático A. Lautman faz uma bela síntese do que está em jogo em seu livro Essai sur les notions de structure et d´existence en  mathématiques.  Ao examinar a dicotomia local-global ele propõe uma alternativa extremamente interessante com consequências tentaculares, referindo à possibilidade de produzir uma síntese orgânica entre diferentes teorias matemáticas que tratam das conexões local-global e que escolhem o predomínio de uma sobre a outra. Lautman argumenta que é preciso estabelecer uma ligação poderosa entre a estrutura do todo e as propriedades das partes de modo a que se manifeste de modo claro e preciso nessas partes a influência organizadora do todo ao qual elas pertencem. Esse ponto de vista, que parece adotar ideias e programas retirados seja da biologia seja da sociologia, pode aparecer na matemática como um procedimento de síntese. Para isso deve-se abandonar o programa de Russel-Whitehead de reduzir a matemática a estruturas lógicas atomísticas; como também a visão de Wittgenstein e Carnap segundo a qual as matemáticas nada mais são do que uma linguagem indiferente ao conteúdo que elas exprimem. De modo semelhante ao que ocorreu na cosmologia relativista na última década com o abandono da axiomatização Penrose-Hawking, que foi estruturada para dar apoio à identificação da existência de um momento único de criação do universo separado de nós por um tempo finito.

Em outro lugar irei me estender sobre esse caminho que Lautman propôs. Aqui, serve somente como citação, como um exemplo de análise do que está acontecendo no território da cosmologia, para apontar que essa questão transcende nosso plano de exame das questões da física e constitui, em verdade, uma área de reflexão em diversos territórios do conhecimento. Ou seja, uma vez mais, nos deparamos com limites incertos de uma questão bem definida em um território que permite uma análise especial em outro território. Embora distintas, essas questões tratam de algo que aproxima os diferentes modos de compreensão da realidade e que constituem o conjunto das ciências, da natureza e humanas. Exemplos concretos dessas ideias têm sido examinados nos últimos anos.

Como disse recentemente, isso coloca a todos nós, físicos, cosmólogos, pensadores de outras áreas, como grandes companheiros em uma caminhada maravilhosa rumo à compreensão do universo, tendo por base a ideia de que a natureza possivelmente está ainda em formação. Não somente em processos e fenômenos, mas na constituição de suas próprias leis.

E surge então a questão, como mudam as leis?  A estabilidade das leis da física observadas em laboratório terrestre decorre do fato que sua dependência temporal envolve tempos cósmicos. Isso significa que somente olhando o universo em grande escala podemos observar esse processo de modificação. Exemplos importantes para detectar essa evolução são a análise da nucleossíntese que determina a abundância dos elementos químicos no universo bem como o exame dos processos que deram origem ao excesso de matéria sobre antimatéria; fenômenos excepcionais, que ocorreram em um estágio extremamente denso do universo, nos primórdios da atual fase de expansão.

Nossa tarefa é examinar como é possível entender solidariedade como a pedra-de-toque para a aplicação da regra de ouro de Lautman na compatibilização entre o micro e o macrocosmo, entre as propriedades das partículas elementares e as características globais, topológicas, do universo.

O modo natural de empreender essa tarefa seria examinar algumas questões formais que requerem desenvolvimento especializado (como a origem da massa, não-linearidade, dependência cósmica das interações, etc.) que deixaremos para um curso mais técnico. Façamos somente um breve sobrevôo da questão.

Há certas dicotomias que são levadas a um exagero em suas representações e importâncias. Isso será feito aqui, em um primeiro momento como uma tática para que possamos discursar livremente e construir de imediato a questão a ser examinada.

Um exemplo típico, que aparecerá frequentemente é a relação entre uma forma de atomismo e o pensamento global, ou de modo mais amplo, entre propriedades locais e características globais.

A física de Altas Energias, dita de partículas elementares, constitui a atual depositária de um discurso arquitetado há muito e que de modo simples iremos provisoriamente descrever como o primado do local.  Com essa denominação sintetizamos diferentes ideias com uma configuração básica comum: a aceitação de que tudo que existe é construído a partir de umas poucas unidades fundamentais. Com o passar dos tempos e a evolução da ciência essas unidades mudam de configuração e seu número pode variar. Eram chamados de átomos nas primeiras décadas do século XX; hoje, são outras formas de elementos fundamentais denominados leptons e quarks.

Em oposição, para simplificarmos a dicotomia forjada nesta batalha, encontra-se o modo global, que iremos simplificadamente identificar pelo termo Cosmologia, a ciência global.

A entrada em cena de um matemático imaginativo: A. Lautman 

A análise de diversos processos físicos, sejam eles originalmente retirados da mecânica teórica, seja de outras áreas da física, faz aparecer um princípio-guia:  a inércia provoca a ilimitada permanência em um estado estável.  Ao aplicarmos esse princípio não somente a partes compactas, regiões limitadas, mas à sua mais completa extensão, o universo, essa entidade  global que ousaríamos chamar provisoriamente de totalidade, produzimos um critério absoluto de constituição das leis físicas, associado a esse tempo ilimitado de existência. Segue então a inesperada concepção  de que o universo persegue (???) o caminho que leva à duração eterna. A quebra da continuidade, com a perda da eficiência da solidariedade (solidária) leva o universo a autodestruição, restando somente o vazio que servirá para outra tentativa de construção de um cosmos, de forjar um mundo. E, assim, indefinidamente.

Podemos então entender o uso do conceito de solidariedade na formulação de Lautman dos princípios da matemática moderna. Trata-se, resumidamente, de conciliar propriedades locais e globais. Para que essa compatibilidade seja bem sucedida, uma troca eficiente de informação deve percorrer o universo. De outro modo, deveríamos aceitar que o controle da evolução do universo estaria dado por um determinismo a priori relacionado a desconhecidas condições iniciais de estruturas locais de equações diferenciais.

Essa solução de compatibilização lautmaniana pode não ter um sucesso  absoluto. Uma tal perspectiva faz surgir a ideia de eficácia limitada da compatibilização lautmaniana. Dito de outro modo, é possível imaginar que o universo tenha passado por várias fases ou ciclos, cada um deles podendo ser caracterizado por um número S (de solidariedade no sentido de Lautman) cujo domínio de valor deve ser posto entre zero e um.  O valor zero sendo o menos solidário, o menos competente na conciliação entre propriedades locais e globais; o valor um sendo o máximo de compatibilidade possível, o limite idealizado de Lautman.

Entendemos dessa forma a aplicação desse critério ao universo. Ele pode ser exemplificado com outras configurações menos abrangentes, como por exemplo, no processo pelo qual um gás ao ser colocado em um frasco se dilui e ocupa todo o volume do recipiente. As forças localizadas se organizam para permitir essa configuração. Podemos também usar procedimentos estatísticos para compreender esse fenômeno. Mas os detalhes local/global não são importantes para essa análise. O que importa é o resultado final que permitiu a conciliação para gerar a dispersão do gás no interior completo determinado pelo frasco que o contém.

Essa compatibilidade não é organizada a priori, mas decorre de processos relativos à relação local-global. A física estatística se ocupa de apresentar uma versão desse processo independente do conhecimento dessa relação, de cada etapa necessária para atingir a situação de equilíbrio final, ou seja, a ocupação completa pelo gás do volume que lhe foi imposto, sua fronteira global.

Para entender de modo simples a compatibilidade da ordem que parte do local para o global e a situação inversa do global para a estruturação do microcosmos vamos nos valer de uma pequena modificação de uma ideia com que Newton exemplificou sua ordenação das leis físicas.

Metáfora do túnel da Mancha

Os engenheiros sabem como conciliar, na construção de um túnel através do mar ou através de uma montanha, ao ser executado simultaneamente a partir de ambos os lados da montanha, para que o encontro dos dois buracos seja harmonioso isto é, que eles se encaixem corretamente.

É preciso técnica e arte para que esses buracos abertos de cada um dos lados da montanha sejam compatíveis em seu encontro, isto é, que ao se encontrarem estejam na mesma altura do solo.

Se um deles estiver, erroneamente, acima do outro então um desvio será necessário fazer. Esse desvio certamente irá provocar defeitos futuros e gastos adicionais não previstos. Para evitar essas dificuldades e tornar todo o processo compatível, os engenheiros devem exercer máxima atenção e competência.

Uma disfunção análoga, associada a este tipo de dificuldade, poderia estar presente também se não houvesse compatibilidade das leis físicas do microcosmo, ao nível das partículas elementares e o macrocosmo, na estrutura global do universo e em particular sua topologia.

Assim como deve existir uma profunda solidariedade, cooperação entre os esforços dos engenheiros de um e do outro lado da montanha, também no universo a solidariedade local-global é fundamental para que perturbações esporádicas não cresçam sem controle, gerando uma condição de instabilidade sem limite. Isso é o que acontece por exemplo no modelo cosmológico de Einstein que foi elaborado tendo como fonte da geometria do universo somente matéria ponderada sem interação entre suas partes sem pressão: a ausência de solidária interação entre suas partes o torna altamente instável.

Um universo que entra em uma fase de expansão controlado por uma aceleração negativa (da variação de seu volume total) — atribuída à força gravitacional atrativa, gerada por matéria ou energia convencional terá inevitavelmente um fim próximo, posto que seu volume começará, cedo ou tarde, a colapsar. Seu futuro, nesse caso, é sua destruição.

Para evitar esse fim, o universo deveria adentrar o modo lautmaniano,  invertendo o sinal negativo de sua aceleração e produzindo uma aceleração positiva que volte a dominar sua evolução.

Essa descrição permite pensar que o universo teria passado por diversos ciclos de expansão e colapso, realizados dentro dos valores possíveis 0 < S <1.

Resumindo, podemos chamar os estados limites dos processos fisicos com nomes emprestados da solidariedade social, ou seja, ao estado S = 0 chamaríamos estado de egoísmo máximo; ao valor S = 1, chamaríamos estado de solidariedade máxima.

Um universo que atinge S = 1 existirá para sempre; um universo com valores de S menores, terá tempos de existência finita que poderão ser determinados pelo correspondente valor de S.

Na teoria das equações diferenciais não-lineares, Poincaré mostrou como é possível existir certas soluções especiais que funcionam como verdadeiros atratores. Isto é, qualquer que seja o início de um processo descrito por essas equações, a probabilidade é grande para que eles terminem como o estado estável que serve de atrator.

Na cosmologia que estamos examinando, uma situação semelhante ocorre, o que leva à questão: essa atração irresistivel de atingir o estado S = 1 afeta a evolução das leis físicas?

A diminuição ou mesmo a ausência da solidariedade local-global estaria associada à instabilidade. Um universo onde S não tem o valor máximo provavelmente seria instável por perturbações que sempre podem ocorrer por flutuações locais, levando-o à autodestruição.  Tal é, por exemplo, o cenário cosmológico estático de Einstein. Sem relação dinâmica entre suas partes ele está fadado a uma limitada existência.

Diferentemente, o universo de Friedman – mesmo possuindo um horizonte, ou seja, mesmo sem ter uma completa conexão entre todas suas partes – permite uma estabilidade maior e a ação de eventuais perturbações não o destroem, mas sim permitem o surgimento de estruturas como galáxias, estrelas, planetas, vida.

O mais fundamental dos princípios que está na base da ciência consiste na hipótese de uma única estrutura espaço-tempo. Uma outra possibilidade admite cenários evolutivos que permitiriam a variação das leis físicas e consequentemente produzir uma história dessas leis concomitantemente com uma história de diferentes universos.

Paradigmas paralisantes ou a desconstrução do real da física: qual a idade do universo? 

Vamos voltar a comentar uma questão das mais instigantes desde sempre na história da humanidade: qual a idade do universo?

A essa pergunta se espera ter como resposta um número, que marcaria o tempo de existência desse universo. Entendemos assim que seria possível datar precisamente sua origem por um tempo finito. Antes de aceitarmos essa possibilidade faremos um pequeno desvio que permitirá colocar essa questão em um contexto mais amplo.

Em verdade, desde tempos primordiais da história humana ela tem obtido inúmeras respostas, através da construção de mitos e crenças religiosas. Recentemente os cientistas, com o ressurgimento da cosmologia científica, em particular a partir da segunda metade do século XX, têm produzido novas respostas.

Embora essas respostas tenham certamente interesse – e algumas são bem fundamentadas – nós não as apresentaremos aqui, não estamos interessados nelas. Também não iremos apresentar uma nova proposta.

Pois o que nos interessa aqui é recolocar essa pergunta crucial, formidável, intrigante, provocadora e excitante, de um outro modo. E, desse novo modo de tratá-la, reduzir sua importância ou melhor relativizar essa indagação ao mostrar que ela não deve ser considerada uma questão absoluta, isto é, isenta de  análise anterior que estabeleça claramente a representação (ou as diversas representações) com que ela pode ser desenvolvida.

Somente como um comentário colateral sobre diversas propostas cientificas recentes que pretendem responder àquela indagação, nenhuma das propostas apresentadas pode ser considerada conclusiva, como comentei no livro Do big bang ao universo eterno.

Comecemos por esclarecer uma questão anterior, a da representação. 

Paradigma da representação 

Aceitar que só existe um mundo conduz a aceitar que deve existir uma descrição única de como ele é, de como ele funciona, quais são as forças que determinam suas estruturas. Não há dúvida de que a ciência provê o mais completo e bem-sucedido procedimento criado para essa função, gerando uma caracterização apropriada do que existe. Deveríamos esperar dessa univocidade a sua identificação com a natureza. Outras formas, racionais ou não, de produzir uma tão completa descrição são consideradas irrelevantes. É precisamente essa univocidade da descrição de cada fenômeno que se tornou uma das características mais atrativas da formulação científica.

E, no entanto, nos últimos tempos essa univocidade tem sido questionada.  Para sustentar essa afirmação teremos que fazer uma incursão por alguns meandros técnicos. Eu procurarei ser menos detalhista possível, sem exigir do leitor um conhecimento maior da ciência. No entanto, sem exibir alguns exemplos, esse discurso fica restrito ao território da opinião, o que não é o caso.

Para isso iremos considerar alguns exemplos esclarecedores tomados da física moderna:

• O mundo quântico pode ser associado a alterações na geometria do espaço tridimensional?
• A presença de qualquer tipo de força pode ser convenientemente eliminada por representação geométrica?
• As utopias controladas geradas dentro de teorias da física são verdadeiras configurações? São partes do que chamamos o mundo real?
• Toda Lei física válida na Terra e suas vizinhanças pode ser extrapolada para todo o universo? Ou, dito de outro modo, as leis físicas são independentes da posição no espaço-tempo?

Estes exemplos, considerados em seu conjunto, tornam o conceito realidade, aquilo que chamamos o mundo real, menos rígido, posto que dependente da descrição.

As diferentes representações, cada uma delas correta e plena no uso de esquemas convencionais da ciência, pode pretender ser a “verdadeira descrição do mundo real”.

Essa multiplicidade, levando à crítica da univocidade do mundo real, foi resolvida pelo establishment pela escolha particular de uma representação, pois os físicos não convivem com esta duplicidade e requerem uma única descrição do real, que quando estabelecida é alçada à condição de paradigma de representação.

O fato de estar sendo feito essa escolha no interior da atividade cientifica lhe confere um satus superior acima de qualquer outra análise seja ela de natureza cientifica ou não.

Essa escolha, racional e arbitrária, é feita sob alguns critérios aceitos universalmente dentre os quais os mais poderosos são a inércia do pensamento e uma desejada simplicidade identificada com a aceitação de que quando nos defrontamos com duas soluções para um dado problema deve-se escolher aquela mais simples, mais econômica.

A necessidade dessa escolha única (de representação do mundo real) não está no mundo, nem está contida na prática cientifica mas sim aparece da angústia associada ao medo de reduzir a força da atividade cientifica, minando o poder controlador sobre o real. Admite-se que a multiplicidade de representações possa enfraquecer o olhar racional sobre o mundo, provocando um efeito indesejado: o deslocamento do real em direção ao caos.

Colocar ordem no mundo (ou, de outro modo, desvendar a ordem no mundo) é escolher de modo seguro e universal um dado paradigma de representação. Único. É precisamente essa escolha, uma prática inerente ao método cientifico, que produz o que entendo por paradigma paralisante.

Ao retirar outras possíveis explicações, outras possibilidades de descrição dos fenômenos, elimina para o presumido sucesso, essa multiplicidade indesejada e complicadora e faz de uma delas sua colagem ao real, que se torna assim, de fato, a definição da realidade.

Talvez fosse necessário nesse ponto enfatizar que não está em questão o processo fenomenológico. O procedimento tradicional da atividade cientifica não está sendo questionado. A questão está em outro lugar, na escolha da mais conveniente dentre várias possibilidades, uma única descrição adequada dos fatos empíricos.

Dito de outro modo, estamos questionando a convicção implícita de que os enunciados científicos sobre as observações que legitimam esse saber não estão isentos da multiplicidade de representações que se pretenderia evitar.  Fez-se um formidável avanço, mas não se realizou a tão esperada e propagada independência de pré-julgamentos e apriorismos sobre o real.

Passou-se do discurso sem fundamentação fenomenológica, da produção política ou religiosa da descrição do real a uma atitude científica de descrição. No entanto, a escolha de representação única dos fenômenos faz entrar pela porta dos fundos o que havia sido expulso ostensivamente pela porta de entrada.

Essa escolha no interior da atividade científica, embora de aparência escamoteada e escondida, é de natureza política.  Isso porque ela ocorre não exclusivamente por adequação e coerência aos processos fenomênicos, mas por uma escolha arbitrária, embora consensual, de uma determinada representação. É essa univocidade que esconde um caráter político.

Chegamos assim a um universo real. E é desse universo, ou melhor de uma representação possível que a pergunta se coloca mais claramente: qual a sua idade? É ele temporalmente finito ou é eterno?

O desvio sobre múltiplas representações enfraquece essa pergunta, pois ela passa a ser entendida como: é esse universo representado do modo como os cientistas colocam, deixando de lado outras representações, finito ou eterno?

Mas que escolha de representação estamos usando para tratar esse universo? Sem especificar esse caminho e essa escolha, a pergunta não pode sequer ser formulada.

Aqui devemos recuperar algumas questões e voltar a examinar o que em outro lugar (Manifesto Cósmico) chamei de utopias controladas. Devemos então entender o processo de bifurcação do universo.

Antes porém uma introdução à metacosmologia se faz necessário, o que faremos na próxima lição.

Apêndice: Comentários quase-técnicos (Restos das leis cósmicas ou das leis físicas às leis cósmicas)

1. Construímos um universo. Organizamos leis cósmicas. Ordenamos sequencialmente observações que descrevemos como extensões de nossos corpos. Vamos além. Impomos que essas leis se refiram a nossos corpos. Produzimos então um mundo.
2. Da redução dos corpos à coleção de átomos, reconhecemos nossa identidade cósmica. Afinal, astrofísicos-poetas sugerem que somos restos mortais de uma estrela e da liberação de carbono ao meio interestelar retiramos parte de nosso ser, a partir destes átomos eternos;
3. E, no entanto, não somos somente isso. Processos complexos intervém e (nos) organizam, a nível elementar, como espécie e como indivíduos. Nossa identidade se forma como única. E como tudo que existe pretende existir eternamente, somos levados a formalizar um Eu para afirmar essa individualidade eterna, que se imagina eterna e que dissimula ter certeza dessa eternidade;
4. É possível pensar assim pois a ciência anuncia que vivemos em um universo eterno, abandonando definitivamente a ideia da singularidade inicial inexplicável associada a um cenário ingênuo e irracional, o nomeado BigBang.
5. O universo impõe seus limites. As forças da natureza, dizemos. Sem nenhuma orientação ulterior. Somente a solidariedade exigida para manter sua longevidade.
6. Aprendemos que elementos fundamentais, como próton e eletron, têm características próprias, mas os físicos não questionam de onde elas vieram. Aceitam como um dado inicial. Os cosmólogos, voltados para a unidade do mundo, vão procurar o que lhes deu esses valores. Por que a massa do nêutron é exatamente essa? Por que a massa do próton é exatamente essa? E muitos outros mistérios como esses acessados na Metacosmologia.
7. Para entender o significado dessas questões é necessário um pensamento global. Isso não implica acesso imediato à solução, mas permite tratar a questão como um significante. Em seguida devemos procurar um compromisso como sugerido por Lautmann, entre o local e o global, explicitando coerências, para só então encaminhar uma resposta.
8. Chega-se assim ao cosmos solidário.