Real e Virtual: uma visão científica
A ideia deste texto, surgiu de um desafio que o Prof. Novello me fez, de fazer uma apresentação dentro de uma série de palestras organizadas por ele, sobre o Real e Virtual, junto com pesquisadores de vária áreas do conhecimento. No meu caso eu deveria falar deste tema em partículas elementares, que é a minha especialização. Mas para isso, apresentarei inicialmente aspectos da mecânica quântica, central no estudo dos fenômenos mais fundamentais da natureza.
Difícil encontrar uma definição consistente que abarque os conceitos de real e virtual, tão umbilicalmente relacionados. Tentar recorrer à filosofia é um trabalho impossível, pois esses dois conceitos têm muitas versões, pelo menos uma para cada filosofo.
Desta forma, definimos de forma pragmática:
– Real, tudo que é possível de ser observado diretamente.
– Virtual, o que não é observado diretamente, mas que tem influência direta nos fenômenos observados.
O Mito da Caverna de Platão pode servir para ilustrar como entendemos estes dois conceitos, um tanto quanto positivista ou operacionalista. Como veremos mais adiante, a mecânica quântica pode ser ilustrada por esse mito, mas subvertendo completamente a ideia de Platão ao formulá-lo.
Para os humanos ali encerrados, as sombras seriam o observado, aquilo que chamaremos de real. Enquanto aquilo que os eventos responsáveis pela criação das sombras, seriam o virtual.
Ao contrário do filosofo que aparece no contexto do mito, o cientista envolvido no estudo da mecânica quântica não sai da caverna, se conforma imaginando o que estaria produzindo aquelas sombras. Para isso cria modelos matemáticos, para este universo inobservável, cujos resultados estejam de acordo com as sombras observáveis.
O objetivo deste texto é dar uma ideia destes dois conceitos dentro da física quântica. Para isso faremos uma definição efetiva de caráter bem fenomenológico, tendo em conta a celebre frase de Heisenberg sobre a ciência: “Temos que lembrar que o que observamos não é a própria natureza, mas a natureza exposta ao nosso método de questionamento”.
Real e imaginário na representação matemática.
Para explicitar o conceito de Real e Virtual em partículas, se faz necessário mostrar alguns elementos da representação matemática usada na teoria quântica. Nesta teoria a dinâmica tem sido representada por equações envolvendo números complexos, enquanto o mundo observável só faz sentido de ser representado por números reais.
Mas o que seria um número complexo? Por definição é um número ou expressão que contém um número real acrescido de um número imaginário. Por sua vez: um número imaginário é um número que, quando elevado ao quadrado, resulta em um número negativo. Lembrando que qualquer número elevado ao quadrado, tanto positivo ou negativo, sempre é um número positivo. O número imaginário conteria o número √-1, também conhecido pela letra i, que ao quadrado i2 = (√-1)2 = -1.
Para um leigo isso parece por demais abstrato, mas ao longo do texto veremos a importância e beleza desta representação matemática.
Os observáveis físicos preditos pela teoria quântica, ou seja, os resultados das experiências, são dados necessariamente por números reais (velocidade, posição, momento angular, etc.). Entretanto as equações que usamos para prever estes resultados, são descritas através de números complexos. Essa aparente dicotomia entre a representação por números complexos e as observações através dos números reais, a torna diferente da teoria clássica, na qual tanto as equações como os observáveis são descritos por números reais.
Para entender melhor aquilo que está sendo dito, apresentamos uma pequena digressão sobre números complexos e números reais. Para os não habituados com a representação matemática, a única coisa importante de entender é que os números complexos não podem representar algo que seja observável pelo ser humano. Nós só observamos a qualquer nível de experimentação (telescópios, microscópios, ou qualquer outro instrumento de medição), algo que quantificamos através de números reais. As quantidades complexas estão presentes na dinâmica das interações, mas não são observáveis.
O grande físico-matemático suíço Leonhard Euler, encontrou uma expressão matemática, extremamente simples e elegante, que relacionava cinco dos principais símbolos matemáticos:
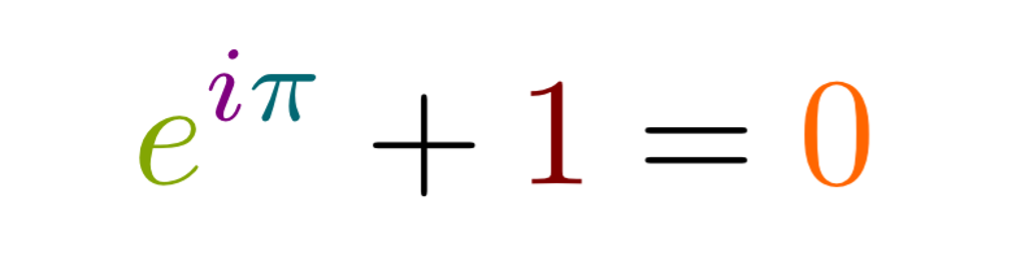
Conhecida como a identidade de Euler. Conta a lenda que ao descobrir essa identidade, Euler exclamou: “Deus existe”.
Realmente é uma coincidência emblemática a de colocar em uma mesma equação: o número neperiano (2,718281828….), descoberto por economistas para contabilizar os juros compostos, com o número pi (3,14159265358979323846…) atribuído a Arquimedes, relacionado à medida de um círculo, além disso essa equação coloca estas duas constantes com os números naturais binários zero e um, a base da matemática criada pelos hindus. Para completar este leque de símbolos desconexos entre si, se inclui nesta equação o número imaginário i = √-1 , que tem uma origem menos determinada, até porque representar o imaginário é de uma abstração que supera a maior abstração até então, que é a de representar a “ausência” através do número zero.
Na verdade, a origem da identidade de Euler foi um caso particular, da equação de Euler, que relacionava a função exponencial com as quantidades trigonométricas seno e coseno na forma:
e ^{i\varphi} = cosseno (φ) + i seno(φ)Para cada valor do ângulo ![]() temos um ponto dentro de um circulo representado geometricamente por:
temos um ponto dentro de um circulo representado geometricamente por:
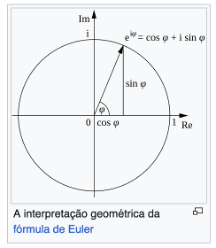
Representação de um sistema clássico.
A primeira parte desta equação (chamada de parte real em oposição a parte imaginária), é suficiente para descrever todos os sistemas clássicos com movimento ondulatório. Ondas de mar, ondas eletromagnéticas, ou mesmo movimentos oscilatórios como um pêndulo, podem ser descritos por esta parte da equação. Basta somente escolher as variáveis corretas para descrição do objeto físico que nos interessa. Se for a evolução temporal, colocamos o tempo como variável, se o interesse for como a onda estará em um determinado lugar, colocamos a variável de espaço.
Claro que estamos falando de um dos muitos aspectos da física clássica, outras representações se fazem necessárias se queremos descrever o movimento de um automóvel, ou de uma pedra sendo lançada no ar. Entretanto, todos estes processos são usualmente descritos através de equações com variáveis, que podem ser observadas como o espaço, o tempo, a velocidade, etc. Inclusive podemos ter equações que possam descrever simultaneamente duas ou mais variáveis.
Um dos casos mais simples de se estudar na mecânica clássica, é o movimento de um corpo. Podemos descrevê-lo através de uma função que permita saber com exatidão, onde se encontra um objeto bem como a sua velocidade, em qualquer tempo que queiramos. Um exemplo prático: a representação de um objeto em movimento, preso em uma mola, pode ser feita através de um gráfico bidimensional, com uma das coordenadas sendo a posição e a outra a velocidade. Podemos representar este movimento no gráfico abaixo por um círculo, onde cada ponto do gráfico representa uma posição e uma velocidade do objeto. Este é o chamado espaço de fase clássico.

Na analogia com o mito da caverna feita acima, os cientistas que desenvolveram a física clássica, desvendaram o mundo real, da mesma forma que o filosofo de Platão desvendou o mundo verdadeiro. O observável contém todas as informações e é completamente descrito por suas equações, onde todos os termos destas são acessíveis diretamente ao estudioso que desta forma vive fora da caverna.
Representação de um sistema quântico.
Em uma passagem da autobiografia de Heisenberg, “A parte e o Todo”, ele descreve o momento em que ele chega às primeiras equações da mecânica quântica da seguinte maneira: “Não pude mais duvidar da consistência e da coerência matemáticas do tipo de mecânica quântica para a qual os meus cálculos apontavam. Fiquei muito assustado. Tive a sensação de que através da superfície dos fenômenos atômicos, eu estava olhando para um interior estranhamente belo…..”.
Na mecânica quântica houve uma mudança radical e pouco compreendida, mas, entretanto, de uma funcionalidade e eficácia espetacular. Essa perplexidade foi expressa recentemente no best-seller de Benjamin Labtut “Quando deixamos de entender o mundo”. Acabou a ilusão de que o Universo obedeceria às regras do que parece lógico para o ser humano. Segundo uma crítica de Reinaldo José Lopes (Estadão 29/02) a este livro, a visão do autor atribui ao aparecimento da mecânica quântica, a perda por parte da humanidade da validade da razão humana para entender o Cosmos, com isso, desapareceria a crença também na nossa capacidade de diferenciar certo e errado, ou o que podemos fazer daquilo que devemos fazer. Exageros à parte, a teoria dos quanta mexeu muito com a cultura. Na verdade, ainda mexe, mas muito menos, pois acabamos nos acostumando a ela.

São vários os aspectos intrigantes que podem ser apresentados por esta teoria. Um dos mais importantes é o princípio da indeterminação de Heisenberg. Este princípio impede sabermos com exatidão a posição e velocidade de uma partícula simultaneamente no nível subatômico.
Importante que se diga, que essa não é uma limitação observacional, como se acreditou por muitos anos, mas uma limitação ontológica, algo inerente ao sistema quântico, independente da existência de um observador. A equação que representaria este princípio seria:
\Delta x \Delta p \geq h
Matematicamente o símbolo grego ![]() representa a diferença de uma variável,
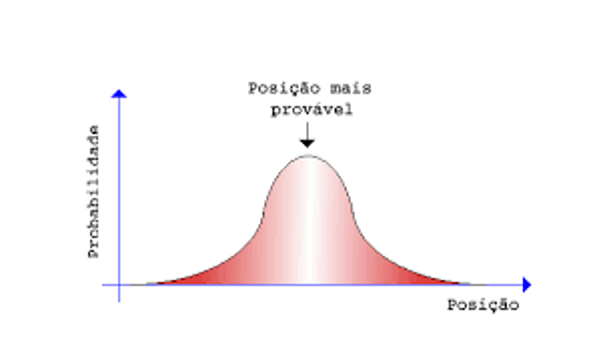
representa a diferença de uma variável, ![]() x, seria a diferença entre dois pontos x1 e x2 , p indica o momento de uma partícula, que nada mais é que a velocidade multiplicada pela massa desta partícula. Finalmente h é a constante de Planck, que é muito pequena, mas diferente de zero (6.58 10-16 eV s). Além de intrigante, essa complementaridade entre as variáveis momento e posição, implica que não podemos ter um espaço de fase entre essas duas variáveis representado por um ponto, como foi mostrado na figura acima. Teríamos no mínimo um círculo de raio h. Cada uma das duas variáveis teria uma distribuição de probabilidade como mostrado abaixo.
x, seria a diferença entre dois pontos x1 e x2 , p indica o momento de uma partícula, que nada mais é que a velocidade multiplicada pela massa desta partícula. Finalmente h é a constante de Planck, que é muito pequena, mas diferente de zero (6.58 10-16 eV s). Além de intrigante, essa complementaridade entre as variáveis momento e posição, implica que não podemos ter um espaço de fase entre essas duas variáveis representado por um ponto, como foi mostrado na figura acima. Teríamos no mínimo um círculo de raio h. Cada uma das duas variáveis teria uma distribuição de probabilidade como mostrado abaixo.
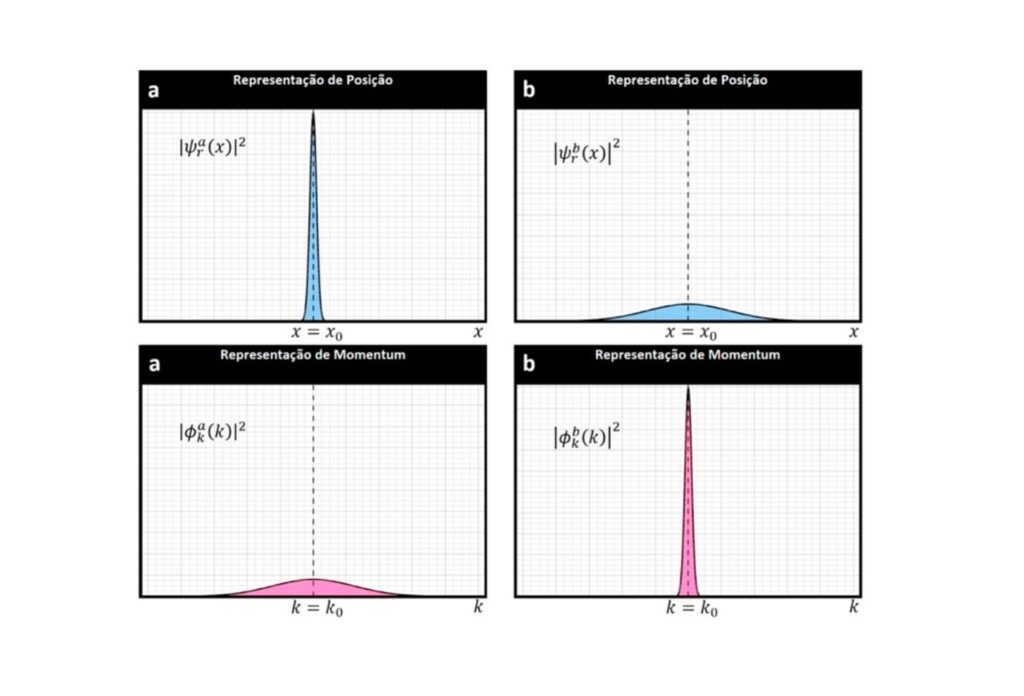
Esse princípio implica em um efeito curioso e estranho aos ensinamentos que tivemos na nossa infância. Aprendemos desde cedo que a ordem dos fatores não altera o produto. Aliás me lembro que ter que decorara esta obviedade clássica. Com a mecânica quântica isso se modifica tendo que ao medimos primeiro a posição com precisão, acabamos alterando o momento e vice-versa. Logo ao medirmos inicialmente o momento p acabamos alterando a posição x, que é diferente de medirmos inicialmente a posição x, que acaba por alterar o momento p.
Esta é uma consequência direta das propriedades do produto das matrizes, que não será aprofundada neste texto. Matematicamente essa propriedade é descrita pela simples equação.
x.p – p.x = ih
Segundo Carlo Rovelli, no seu livro Helgoland, uma biografia de Heisenberg, na prática tudo que foi feito por ele e seus colaboradores, foi acrescentar à física esta equação, extremamente simples na forma, mas de extrema obscuridade no seu significado.
São inúmeras as consequências geradas por esta teoria: a quantização dos níveis de energias em um átomo, aquilo que Bohr chamou “O milagre da estabilidade da matéria”. Os efeitos de interferência construtivas e destrutivas, semelhantes as observadas nos fenômenos ondulatórios, o efeito de saltos quânticos em barreiras de potencial, essas entre outras tantas estranhezas geradas por esta teoria. Com efeitos enormes na tecnologia, desde os semicondutores até a energia nuclear.
O preço a ser pago por esta formulação não foi pequeno. Em um diálogo entre Heisenberg e Einstein, este último, um conhecido crítico desta teoria, dizia que a mecânica quântica era aquilo do que sabemos da natureza e não aquilo que a natureza faz. Em resposta Heisenberg ponderou que nunca os cientistas conseguiriam chegar sozinhos a essas equações: “se elas foram reveladas pela própria natureza, seria uma forte sugestão de que elas devem fazer parte da própria realidade, e não apenas as nossas ideias sobre a realidade”.
Os efeitos de interferência advindos da mecânica quântica, muda um dos pilares do pensamento ocidental, onde as propriedades de um objeto são determinadas pelas suas próprias características. No caso quântico as propriedades de um objeto estão também relacionadas com a interação com os outros objetos. Ou seja, as possíveis interações com os objetos existentes no universo é parte inseparável dos objetos.
Isto pode ser entendido dentro da filosofia de Leibniz, onde todas as propriedades de um objeto são relações a outros objetos. Aliás, algo igualmente presente na relatividade introduzida por Einstein, onde só faz sentido pensar um objeto em relação a outro.
Existem inúmeras interpretações para os fenômenos quânticos, que estão fora do escopo deste artigo. Mas para se ter uma ideia da dificuldade, abaixo apresento um diagrama das várias correntes existentes em função da popularidade de cada uma e em função do tempo, segundo a visão do Prof. Osvaldo Pessoa Jr. professor de filosofia da USP.
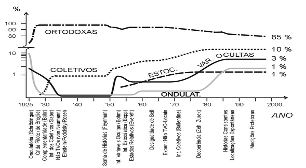
Necessidade de números complexos para descrever a mecânica quântica
Apesar de seu papel fundamental na matemática, não se esperava que os números complexos tivessem um papel semelhante na Física por conta da parte imaginária. E, de fato, antes da teoria quântica, a mecânica de Newton ou o eletromagnetismo de Maxwell usavam números reais para descrever como os objetos se movem ou como os campos eletromagnéticos se propagam, As teorias às vezes empregavam números complexos para simplificar alguns cálculos, mas seus axiomas só faziam uso de números reais.
Isso muda radicalmente na teoria quântica. Desde as suas primeiras propostas, a conhecida equação de Schroedinger e a chamada mecânica matricial de Heisenberg –que completam neste ano ambas cem anos– o termo complexo está presente nestas duas formulações. Inicialmente se imaginou, inclusive pelo próprio Schroedinger, que a presença do termo complexo seria simplesmente um truque matemático. Com o passar dos anos, esse aparente artifício matemático, foi se consolidando como algo mais fundamental.
Recentes estudos teóricos e experimentais apresentam indicativos, que nenhuma teoria quântica usando somente equações com números reais, daria conta de certos fenômenos observáveis
(ver por exemplo os artigos recentes; Física quântica exige números complexos – e sempre terá uma parte imaginária:https://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=teoria-quantica-exige-numeros-complexos&id=010130211217, Quantum Mechanics Must Be Complex https://physics.aps.org/articles/v15/7).
Como vimos, o quadrado de um número imaginário é um número real. Isso quer dizer que só teremos acesso ao quadrado dos valores obtidos, através das soluções das equações da mecânica quântica, quando é possível comparar com o observável experimental. Desta maneira estamos acessando somente o resultado de um processo dinâmico e não a dinâmica em si, como na física clássica. Ou seja, como dissemos no início, observamos as sombras, o Real, o Imaginário seria a dinâmica subjacente, representado por uma equação com termos complexos como a equação de Euler.
Partículas reais e virtuais.
O processo de colisão entre partículas livres muito energéticas é governado pela mecânica quântica relativística. Essa teoria pode ser aplicada nos vários tipos de interações entre partículas fundamentais: a eletromagnética entre partículas com carga elétrica, bem como nas interações fracas responsáveis pelas desintegrações nucleares.
A ideia básica desta teoria, é de que duas partículas interagem trocando uma terceira partícula virtual, que pode ter massa tanto positiva como negativa. Essa ideia simples é explicitada na figura abaixo. Quando uma pessoa joga uma bola com massa positiva ela se afasta, assim como aquela que a recebe também se afasta. A bola seria a mediadora de uma força repulsiva. Se a bola possui uma massa negativa, ocorreria exato o contrário, neste caso a bola seria a mediadora de uma força atrativa.

Claro está, que isso é uma representação possível em um mundo virtual onde vive a mecânica quântica. No mundo real, das observações, não existe massa negativa. A “bola” quântica é representada por uma função com números complexos, com características peculiares para cada tipo de interação. Para as interações eletromagnéticas, a bola é representada pelo quantum de luz, que é o fóton. Nas interações entre quarks, a “bola” é um glúon, nas interações fracas temos dois tipos de “bola”, o bóson W e o Z. Uma forma muito usada de representar este processo foi proposto por Feynman, como mostrado na figura abaixo.
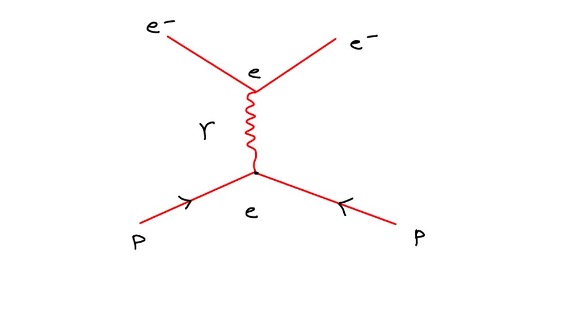
Um elétron livre interagindo com um próton igualmente livre, emite um fóton virtual que é absorvido pelo próton. Como tem cargas oposta eles se atraem, logo o fóton virtual, responsável pela interação, deve ter massa negativa. Se a interação fosse entre um pósitron (antielétron) e um próton, que tem a mesma carga, esse fóton iria ter massa positiva.
Partículas observáveis e não observáveis
Das partículas responsáveis pelas interações, que acima chamamos de “bolas”, somente o fóton é observado diretamente, as outras são observadas indiretamente. Na família das partículas, temos uma outra chamada de hadrón, que é um nome genérico que se dá para aquelas partículas que sofrem interações fortes. Em uma perspectiva elementar elas são formadas por quarks que interagem através dos glúons. Mas para o nosso propósito o que importa é que elas interagem entre si. Os hadróns mais conhecidos são o próton e o nêutron, além desses, temos dezenas de outras partículas pertencentes a esta família.
Tanto o próton como o nêutron podem ser observados diretamente por detectores de partículas, pois tem tempo de vida suficiente para poderem atravessá-lo e serem identificados sem maiores dificuldades. Mas são poucas as partículas que têm tempo de vida suficiente longo para atravessar um detector de partículas, que em geral medem mais de vinte metros de comprimento.
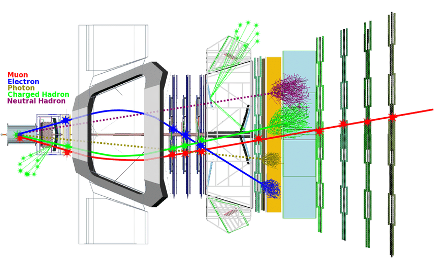
Na prática somente partículas com tempo de vida maior que um milionésimo de segundo é que conseguem atravessar todo o detector e serem identificadas. Além do próton e do nêutron, existem os mésons ![]() e kaons, além do elétron e o seu parente mais massivo o múon. Importante dizer que essas partículas produzidas em aceleradores, viajam a velocidades próximas da luz, por isso apesar de tempos diminutos de milionésimo de segundo, são suficientes para atravessarem um detector, devido a dilatação temporal que ocorre em objetos relativísticos. O restante das outras partículas, tem tempo de vida tão pequenas, que mesmo nestas velocidades, não conseguem chegar aos diferentes detectores para serem identificadas. Para se ter uma ideia, uma família de partículas conhecidas como “charmosas”, têm tempo de vida média de um trilionésimo de segundo e caminha da ordem de um centímetro dentro de um detector quando produzida a velocidades próxima da velocidade da luz (300.000Km/s).
e kaons, além do elétron e o seu parente mais massivo o múon. Importante dizer que essas partículas produzidas em aceleradores, viajam a velocidades próximas da luz, por isso apesar de tempos diminutos de milionésimo de segundo, são suficientes para atravessarem um detector, devido a dilatação temporal que ocorre em objetos relativísticos. O restante das outras partículas, tem tempo de vida tão pequenas, que mesmo nestas velocidades, não conseguem chegar aos diferentes detectores para serem identificadas. Para se ter uma ideia, uma família de partículas conhecidas como “charmosas”, têm tempo de vida média de um trilionésimo de segundo e caminha da ordem de um centímetro dentro de um detector quando produzida a velocidades próxima da velocidade da luz (300.000Km/s).
Partículas ressonantes.
As partículas são caracterizadas pela sua massa, momento angular intrínseco e o tempo de vida. O próton tem momento angular ½ e tempo de vida infinito, assim como o elétron, A diferença é que a massa do próton é cerca de duas mil vezes maior que a do elétron e eles tem cargas iguais, mas opostas. Já o múon, píon, kaon e o nêutron, acima citados, tem um tempo de vida limitado, e se desintegram produzindo outras partículas de massas inferiores.
Dentro da família das partículas, existe uma grande quantidade delas, conhecidas como partículas ressonantes. Existem ressonâncias de vários tipos, com diferentes momento angular, diferentes massas. O que caracteriza esta classe de partículas é o tempo de vida menor que a constante de Planck (6.58 10-16 eV s). Isso implica que se usamos a indeterminação de Heisenberg para a correlação entre tempo e energia, partículas com estas características têm uma indeterminação no valor da sua massa (lembrando que massa e energia são iguais, a menos de uma constante, que é da velocidade da luz ao quadrado ![]() ).
).
A única forma que conhecemos de representar partículas com indeterminação na massa, é através de uma função complexa. Portanto podemos dizer que são partículas virtuais, e têm sua existência somente nas interações, como no caso do fóton virtual descrito acima. Ou seja, ressonâncias só têm existência no universo quântico, não são observáveis físicos diretos.
O fato de não serem observadas diretamente, não retira a importância da sua existência. Elas são essenciais para podermos entender a natureza e as interações entre as partículas observadas. São responsáveis pela geração de massa dos quarks, como o famoso bóson de Higgs, ou mesmo a geração da massa do próton, como é o caso do méson sigma, que também tem um papel importante nas interações nucleares. Além é claro das chamadas interações fracas, através do bóson W, responsáveis pela desintegração dos quarks u e d, bem como os quarks top, o beauty, ou mesmo o charm, as partículas mais fundamentais, que fazem parte da formação da matéria.
Apesar destas ressonâncias, serem virtuais e representadas por uma função complexa, elas podem ser observadas indiretamente através de uma importante propriedade da relatividade. Segundo essa teoria, a combinação entre o momento e a energia de uma partícula, se elevado ao quadrado nós fornece a massa da própria partícula.
mc^2 = \sqrt{E^2 - (pc)^2}Uma das bases mais solidas da física é de que tanto a energia como momento, são quantidades conservadas em sistemas isolados. Portanto se a ressonância de massa mc2 se desintegra em duas outras partículas de menor massa, as duas carregaram todo o momento e energia da partícula “mãe”. Se as duas partículas filhas, forem algumas das partículas listadas acima, capazes de atravessar todo o detector, se pôde através deste aparato, ter todas as informações relativas ao momento e energia delas e assim calcular a massa da ressonância “mãe”.
Como a massa é um invariante relativístico, ou seja, é sempre a mesma independente em que referencial foi medido, isso permite podemos ter além das massas da partícula a sua largura, esta última relacionada a indeterminação no valor da massa, devido ao princípio de Heisenberg.
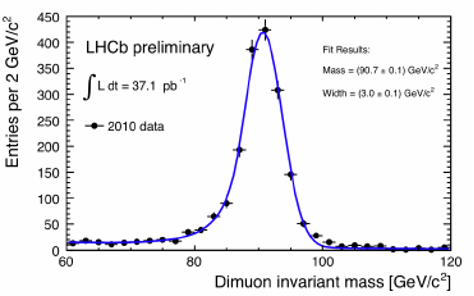
Na figura acima, vemos a distribuição de massa das filhas, que nominamos como “massa invariante”: um múon negativo e um múon positivo, provenientes da desintegração de uma partícula Z0. A massa dessa ressonância é de 90.7 GeV, a sua largura, ou incerteza é de 3.0 GeV. A função em azul, que descreve a distribuição destes eventos, é o quadrado da função complexa, que descreve as ressonâncias, conhecida como Breit-Wigner:
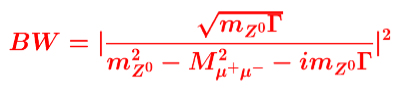
Onde Mz0 é a massa da ressonância, ![]() é o resultado do cálculo da massa invariante das duas filhas, gama é a largura da ressonância ou incerteza na massa, que aparecem multiplicados pelo número imaginário i. Como estamos representando valores reais obtidos nos detectores de partículas, esta função deve ser elevada ao quadrado, para torná-la real.
é o resultado do cálculo da massa invariante das duas filhas, gama é a largura da ressonância ou incerteza na massa, que aparecem multiplicados pelo número imaginário i. Como estamos representando valores reais obtidos nos detectores de partículas, esta função deve ser elevada ao quadrado, para torná-la real.
Interferência entre partículas ressonantes.
No exemplo acima, a complexidade da função desapareceu ao elevarmos ao quadrado a função Breit-Wigner (BW). Essa operação não apresentou nenhuma dificuldade e nenhum efeito quântico que justificasse a presença de uma equação complexa, para representar a ressonância a não ser a existência da largura da mesma. Ou seja, poderíamos sem perda de rigor científico representar a ressonância diretamente por uma função real.
Entretanto a complexidade da BW tem um papel fundamental, se tivermos duas ressonâncias dividindo parcialmente a mesma região da massa invariante, neste caso aparece um novo termo que chamamos de interferência. Na mecânica quântica não basta conhecer os dois objetos individualmente para termos o conhecimento do sistema completo. Ou seja, mesmo que saibamos tudo relativo a um objeto, uma ressonância no nosso caso, se este objeto interagiu com outra ressonância, deixamos de conhecê-lo completamente, a menos que saibamos também como ele interage com o outra. A relação entre as duas ressonâncias não é necessariamente algo que esteja contido em um ou no outro, é algo que vai além das características de um ou do outro.
Se voltarmos a nossa equação mais geral que representa a amplitude complexa de um sistema quântico, podemos entender melhor a razão dela ser complexa.
e^{i\varphi}=cosseno(\varphi)+ i\ seno (\varphi)Podemos dizer que a sua parte real (![]() ), representaria o objeto em si, com as suas propriedades individuais. A parte imaginária por outro lado, representaria a interação dela com o universo. Se ela se encontra isolada ou mesmo se fossem duas ressonâncias clássicas, como na figura abaixo, não seria necessário a presença do termo imaginário.
), representaria o objeto em si, com as suas propriedades individuais. A parte imaginária por outro lado, representaria a interação dela com o universo. Se ela se encontra isolada ou mesmo se fossem duas ressonâncias clássicas, como na figura abaixo, não seria necessário a presença do termo imaginário.
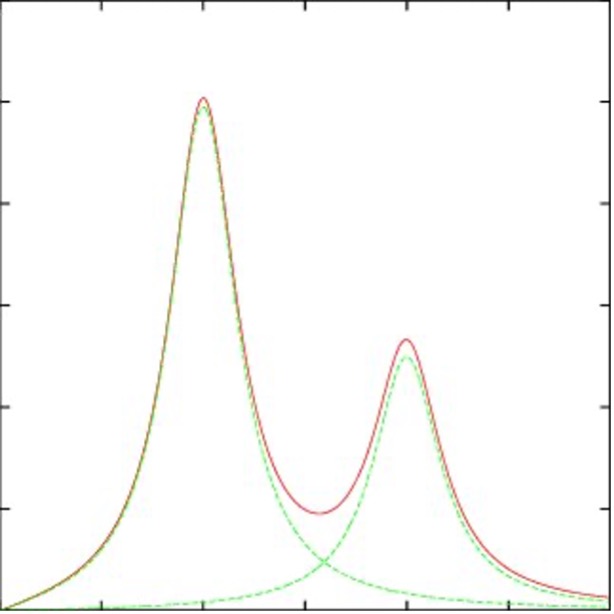
Duas ressonâncias clássicas ocupando parcialmente a mesma região da massa invariante. https://arxiv.org/pdf/1206.0865.pdf
Entretanto, o termo imaginário cria as condições para aparecer os termos de interferência quântica entre as duas ressonâncias. Surge então uma terceira entidade, que não está contida nem na primeira e nem na segunda ressonância, mas um terceiro objeto que existe somente pela interação entre as duas ressonâncias. De fato, existe um bem estabelecido teorema, conhecido como teorema ótico, que relaciona diretamente a parte imaginária da equação acima, com a interação entre partículas.
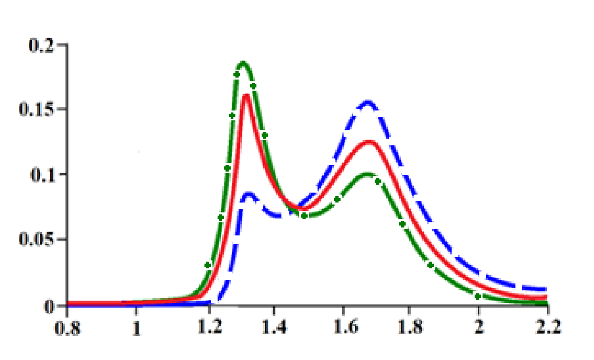
Duas ressonâncias quânticas ocupando parcialmente a mesma região da massa invariante.
Três distribuições possíveis em função da natureza da interferência.
Para se entender a dimensão do termo de interferência, Carlo Rovelli usa uma bela analogia: “Tanto o cubismo quanto a teoria quântica se afastam da ideia de que o mundo é figurativamente representável. Pinturas cubistas muitas vezes sobrepõem imagens incompatíveis de um objeto ou pessoa, representada sob diferentes pontos de vista. Da mesma forma, a teoria quântica reconhece que medições de diferentes propriedades do mesmo objeto físico pode não ser conciliável.”
O problema de três corpos.
Tanto a física clássica, a relatividade, bem como a mecânica quântica, tem excelentes resultados, dentro das suas limitações é claro, quando descrevem a dinâmica de um ou dois corpos. Acrescentar um terceiro corpo nestas teorias bem estabelecidas, é sempre uma complicação não trivial de ser resolvida. A série da Netflix “O problema de três corpos”, baseado no romance do chinês Liu Cixin, espelha bem esta dificuldade.
Nesta série mostra, que mesmo se tratando da gravitação de Newton, uma das teorias mais bem estabelecidas, a presença de outros sóis dificulta a estabilidade do sistema e o problema se torna muito difícil de resolver, senão impossível. No caso do nosso sistema Sol, Terra e Lua, é possível resolver aproximadamente, pois as diferenças de massa entre estes três corpos são muito grandes. Devido a estas diferenças, podemos fazer uma boa aproximação, criando um par de sistemas de dois corpos. Isto tem permitido a estabilidade do sistema e boas previsões teóricas sobre o comportamento do movimento destes corpos, com boas previsões, tanto do movimento das marés como dos eclipses.
Essa simplificação de um problema complicado é marca registrada da pesquisa em física. Chamamos esta prática de fatoração do problema. Isolamos uma parte do mesmo e depois verificamos qual a validade da aproximação feita.
Neste sentido, temos estudado processo de desintegração de uma partícula de massa alta, como são os mésons com charm, ou com beauty, que tem massas suficientes para produzirem três partículas de menor massa, partículas 1,2,3.
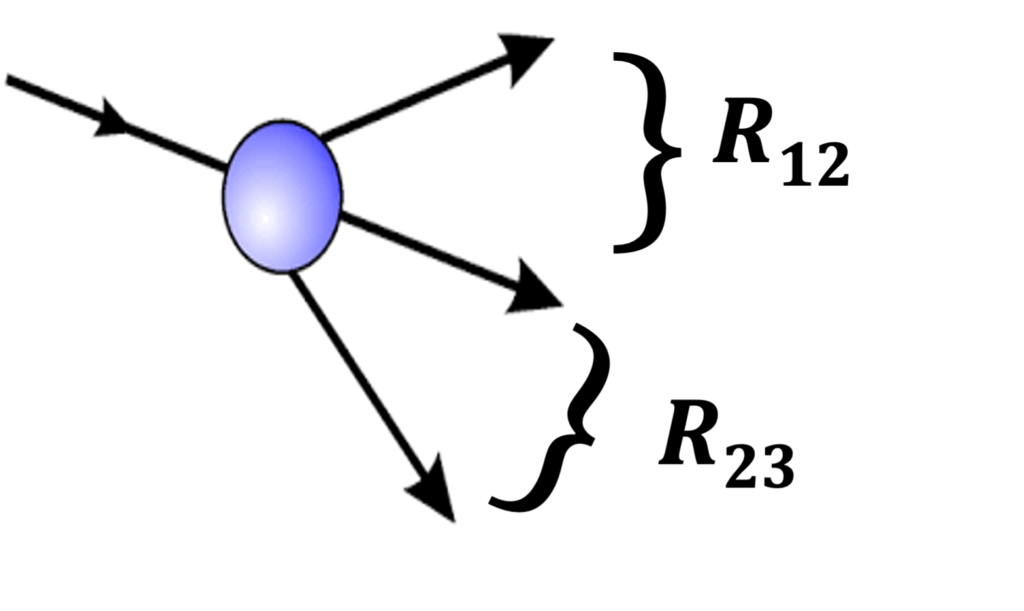
Para o sistema das partículas 1 e 2, podemos encontrar ressonâncias que chamamos de R12, já se juntamos as partículas 2 e 3, teremos a possibilidade de encontrar ressonâncias do tipo R23. Ë possível que em determinadas regiões de energia, a partícula 2 pode estar tanto na ressonância R12, como na R23. Classicamente isto seria impossível, mas no mundo quântico isso é viável e mais que isso, as ressonâncias R12 e R23, podem interferir, tanto de uma forma construtiva como de uma forma destrutiva. Se as duas forem igualmente prováveis nesta região de energia, elas podem aparecer como quatro vezes mais intensa que nas suas vizinhanças, ou mesmo podem se anular e aparecerem com intensidade zero nesta mesma região. Como mostra estas simulações mostrada nas figuras abaixo. Elas representam duas ressonâncias que se encontram de uma forma perpendicular, vermelho representa forte intensidade, azul pouca. Na figura da esquerda temos interferência construtiva, onde as duas se encontram de forma construtiva e intensidade se multiplica por 4, em relação aos outros pontos fora da região de interferência. Já a figura da direita apresenta uma interferência destrutiva, onde a região do encontro delas, fica anulado, com intensidade zero.
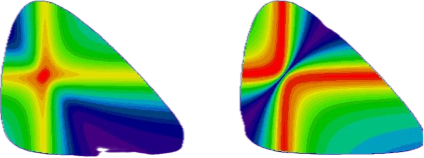
A paleta de cores, assemelhando o espectro de luz, não foi por acaso. A ideia de associar as interferências quânticas com as interferências da luz, está muito presente na tentativa de simular os efeitos quânticos, já que ambos sofrem interferências e dispersão.
Epilogo.
Na concepção da palestra, a minha maior preocupação não foi a de tentar explicar a Mecânica Quântica para leigos, algo de extensa literatura. A linha que adotei neste artigo, foi a de mostrar de forma mais clara possível, quais as dificuldade e limites, existentes na própria comunidade de físicos de compreender esta teoria. Além é claro de mostrar algumas implicações no mundo das partículas relativísticas.
O grande físico e divulgador científico, Richard Feynman, dizia que “quem diz que entende a mecânica quântica”, não tinha entendido a mesma. Outro grande físico, prêmio Nobel, Weinberg, faz uma bela comparação entre o conhecimento da mecânica quântica nos dias de hoje, com a teoria da gravitação de Newton, na época em que foi formulada. Massa atrai massa na razão direta delas e inversa do quadrado da distância, foi uma descoberta sensacional, que explicava nesta simples equação, tanto o movimento planetário em torno do Sol, como uma pedra lançada por menino em uma briga de rua. Mas o mesmo Newton se perguntava, como que a matéria no centro da Terra, sabe da matéria no centro da lua? Para Weinberg, a nossa compreensão sobre a mecânica quântica, se encontra no mesmo estágio que a gravitação para Newton. Esta ideia segue no mesmo caminho do questionamento do Einstein no diálogo com Heisenberg, mencionado anteriormente, onde a mecânica quântica descreve “aquilo que sabemos da natureza”, falta saber “aquilo que a natureza faz”.
Um ponto de vista oposto, pode ser entendido dentro da filosofia de Nietsche, onde não se pode atribuir leis à Natureza, quem tem leis são os homens. Por isso, seria inútil tentar saber o que a “natureza faz”, através de alguma lei, como em geral a ciência procura fazer. Portanto o máximo que podemos esperar da ciência é a de encontrar uma boa representação dos fenômenos observados na Natureza. Essa filosofia é algo parecido com a resposta que Heisenberg fez ao questionamento de Einstein, onde a realidade foi revelada pelos experimentos e a teoria quântica simplesmente as representou.
Sendo assim, com tantos sucessos nas descrições dos fenômenos observados, com acordos excepcionais entre previsões teóricas e resultados experimentais, além de infinitas aplicações tecnológicas bem-sucedidas, temos na mecânica quântica uma eficiente representação da Natureza. Será isso suficiente? De qualquer maneira, é difícil aceitar com tranquilidade, que a ordem dos fatores possa alterar o produto.
