David Bohm: Físico, Pensador, Transgressor

Introdução

Para além da Física, David Bohm foi um dos grandes pensadores do século XX. Ao se examinar o livro celebrando seu septuagésimo aniversário (referência 1), vemos não só contribuições de importantes e influentes físicos, como também textos de filósofos, biólogos, neurocientistas, psicólogos e artistas, todos relatando a relevância das ideias de David Bohm para os seus trabalhos. Isto mostra a complexidade e abrangência do seu pensamento. Nesta minha contribuição, inserida no tema que aborda os transgressores da Física, vou me concentrar na atuação de Bohm na Física, onde ele questionou e propôs alternativas concretas e consistentes ao pensamento dominante sobre Mecânica Quântica, desafiando alguns dos mais proeminentes físicos da época. Como uma outra de suas transgressões ao pensamento da época foi justamente afirmar que a Física não se esgota em si própria, que é necessário um diálogo com outras áreas do pensamento, procurarei resumir, ao final, algumas de suas ideias metafísicas, dentro das limitações do meu conhecimento sobre o assunto. Neste terreno, sugiro fortemente ao leitor interessado que se aprofunde lendo Bohm diretamente (referências 1, 2 e 3). Sobre sua vida e a inserção de sua teoria quântica em relação a outras propostas, vejam as referências 4 e 5.

Os primeiros anos, a formação em Física, e o período em Princeton

David Bohm nasceu em 1917, na Pennsylvania, EUA. Ele logo se encantou com a Astronomia, o que não agradou seu pai, um bem-sucedido comerciante de móveis. Bohm ainda tentou entrar no ramo do comércio, inclusive realizou uma pequena invenção que muito o orgulhava, mas não conseguiu vender uma peça sequer de seu invento. Decidiu então se tornar um físico teórico. Doutorou-se em 1943, em Berkeley, sob a supervisão do famoso físico norte-americano Robert Oppenheimer, diretor do Projeto Manhattan, que tinha por finalidade construir a bomba atômica americana. Sua tese tratava do espalhamento de partículas nucleares (prótons e dêuterons). Por ser uma pesquisa com implicações para o Projeto Manhattan, sua tese foi considerada sigilosa e não poderia ser apresentada em público, nem tampouco para o Projeto Manhattan, pois Bohm tinha ligações com o Partido Comunista Americano. Dado o impasse, o título de doutor foi-lhe dado graças à palavra e prestígio de Oppenheimer, garantindo que sua tese era muito boa.

Ainda em Berkeley, investigando o comportamento de elétrons em gases, percebeu comportamentos coletivos que conseguiu descrever matematicamente, dando contribuições muito importantes para a compreensão da física da plasmas. Ficou conhecido, e com carta de recomendação de Oppenheimer, conseguiu o posto de professor assistente em Princeton.

Bohm chegou a Princeton em 1946. Logo lhe foi pedido para ministrar cursos de Mecânica Quântica, quando foi se dando conta das inúmeras imprecisões da formulação padrão desta teoria (denominada interpretação de Copenhaguen, por ter sido liderada pelo físico dinamarquês Niels Bohr). Decidiu então organizar suas ideias escrevendo um livro sobre o assunto, abordando aspectos físicos pouco comentados. Terminou este livro em 1951, com o título “Quantum Theory” um clássico no assunto. Mas como funciona esta formulação padrão? Vejamos como esta interpretação entende um dos mais estranhos fenômenos do mundo quântico, a interferência quântica.

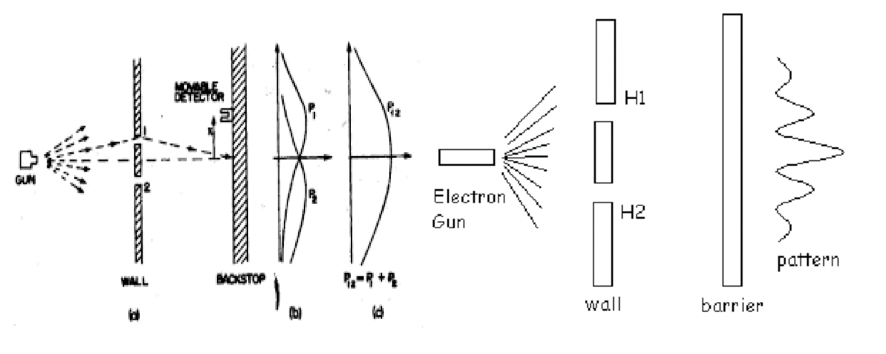
Seja o experimento da fenda dupla, onde um canhão lança elétrons sobre uma parede por onde eles só podem passar através de duas fendas. Os elétrons, um a um, são depois absorvidos por um anteparo mais adiante, como mostrado na figura 1. Se fecharmos uma das fendas e lançarmos a coleção de elétrons pelo sistema veremos uma maior quantidade de elétrons chegando no anteparo na região da direção do orifício aberto. Se fecharmos a outra fenda, vemos a mesma figura, mas seu ponto de maior intensidade será deslocado para a direção do centro do outro orifício aberto. Ao deixarmos as duas fendas abertas, esperaríamos encontrar a soma das duas figuras já que, num raciocínio clássico, os elétrons passam por uma fenda ou pela outra (lado esquerdo da figura 1). Entretanto, a figura obtida é completamente diferente, típica de uma figura de interferência de ondas (lado direito da figura 1), e a pergunta por onde passou o elétron parece não ter resposta:

1. Se passou por um dos dois caminhos não teríamos a figura de interferência, como discutido acima.
2. Passou pelos dois caminhos? Mas se colocarmos dois detectores, um em cada caminho, só um deles registra a passagem do elétron!
3. Não passou por nenhum caminho? Mas se bloquearmos os dois caminhos, nada é registrado!

A solução de Copenhaguen para este aparente paradoxo é a seguinte: não faz sentido falar de trajetórias ou por onde o elétron passou sem que haja um aparelho de medida que efetivamente decida sobre estas questões. Não existe realidade objetiva, isto é, independente das observações. Propriedades quânticas são potencialidades que só se realizam em uma medida.

As potencialidades são descritas por uma onda que depende do espaço e do tempo, ψ(x,t), que é complexa. Seu módulo ao quadrado,|ψ(x,t)|² , fornece a probabilidade de encontrar a partícula na posição x e tempo t após uma medida. No experimento da fenda dupla, temos as potencialidades de o elétron passar pela fenda 1 ou pela fenda 2,  ψ = ψ₁  + ψ₂. Assim, |ψ|² = |ψ₁|²  + |ψ₂|² + ψ₁^*ψ₂ + ψ₁ ψ₂^*. Os dois últimos termos são os responsáveis pela interferência quântica, que aparece na figura 1.

A interpretação de Copenhaguen foi construída sob a influência das ideias positivistas do começo do século passado, cristalizadas no Círculo de Viena dos anos 1920. Para os positivistas, a única forma de adquirir conhecimento é através do método científico: afirmações, conceitos ou hipóteses que não possam ser testadas pela observação experimental não têm sentido. A ideia da existência de uma realidade independente da percepção humana jamais poderá ser testada por nós, humanos, já que sempre haverá a intermediação dos nossos sentidos sendo, portanto, uma hipótese fútil.

Dadas estas premissas filosóficas, fica mais fácil compreender a postura de físicos como Bohr, Heisenberg e tantos outros a respeito dos fenômenos descritos acima. Nada será acrescentado aos fatos tais como eles nos aparecem. Portanto, não se pode atribuir qualquer propriedade a uma partícula quântica antes que esta propriedade seja efetivamente observada (elétrons que passam pela fenda 1 só adquirem a propriedade de passar pela fenda 1 se forem observados passando pela fenda 1).

Vemos, portanto, segundo eles, que não faz sentido conjecturar por onde caminha o elétron na experiência descrita anteriormente já que as diferentes possibilidades (passar pela fenda 1 ou pela fenda 2) não foram verificadas experimentalmente. O caminho só pode ser determinado se o artefato experimental for construído para isso (colocar um detector de elétrons num dos caminhos), e neste caso o resultado final é compatível com essa determinação (distribuição de elétrons no anteparo sem as franjas de interferência, lado esquerdo da figura 2). Conclui-se, dentro desta interpretação, que não se pode atribuir estados de realidade às partículas quânticas independentemente da observação humana.

Segundo Bohr, o objetivo fundamental da ciência não é compreender a natureza tal como ela é, mas tão somente entender o que obtemos quando realizamos experimentos. Os conceitos que entendemos e podemos comunicar aos nossos pares são clássicos, e como tal qualquer teoria científica deve ser formulada em termos clássicos. Assim, um aparelho de medida deve necessariamente ser clássico já que seus resultados devem ser passíveis de compreensão e comunicação por nós, humanos. No centro da investigação científica estão os conceitos clássicos que nos orientam. Em direção ao domínio quântico, apenas alguns deles podem ser aplicados, por vez, de acordo com o que se está perguntando sobre o sistema (complementaridade). A medida é a interação entre o aparelho de medida clássico e o objeto quântico. Esta interação é objetiva e impossível de ser analisada. Se tentarmos descrever quanticamente um aparelho de medida e suas interações com algum sistema físico, ele não seria mais um aparelho de medida, por definição. Qualquer hipótese sobre esta interação só faria sentido, segundo o pensamento positivista, caso pudéssemos testá-la experimentalmente. Mas neste caso, um outro aparelho de medida clássica deveria ser inserido no processo, necessariamente alterando a configuração anterior.

O esquema conceitual de Bohr é excessivamente inflexível, quase autoritário: não se pode analisar um processo de medida, não se pode perguntar detalhes sobre os fenômenos quânticos, não se pode indagar sobre uma dinâmica sub-quântica, não há nada que possa ir além da complementaridade dos conceitos clássicos. Na verdade, essa intransigência resulta de um poderoso processo de indução totalmente injustificado e contraproducente: como poderemos verificar estas afirmações sem examinarmos as consequências de esquemas teóricos onde elas não são verdadeiras? Não contestá-las seria acreditar nestas impossibilidades como um dogma, o que é anticientífico. Felizmente, vários outros físicos, mesmo alguns inseridos na interpretação de Copenhaguen, não se satisfizeram com este esquema. Imagina-se que tudo seja formado por átomos, inclusive os objetos clássicos, então em que momento se efetua exatamente esta separação entre clássico e quântico?  Certamente não é uma questão de tamanho (o objeto ser macroscópico ou microscópico) uma vez que existem alguns objetos macroscópicos que se comportam quanticamente. O físico austríaco Erwin Schrödinger levantou uma questão importantíssima em relação ao limite clássico: se existem funções de onda que descrevem muitas partículas, sem limites para a sua quantidade, porque então não vemos interferência quântica em objetos macroscópicos, como a causada pela interferência entre a função de onda descrevendo um gato vivo em superposição com a função de onda descrevendo um gato morto (o famoso gato de Schrödinger)? Esta é uma questão extremamente relevante, deixá-la sem resposta torna a teoria vaga e imprecisa. Além disso, temos duas leis de evolução, uma dada pela equação quântica (equação de Schrödinger) que rege a dinâmica função de onda do mundo quântico com a qual todos estavam de acordo, e as leis clássicas que governam os aparelhos de medida.

Bohm considerou esta formulação bastante insatisfatória e imprecisa. Em Princeton, teve várias conversas com o físico alemão Albert Einstein sobre o assunto, que era diametralmente oposto à visão de Ciência defendida por Bohr. Para Einstein, o cientista deve assumir como hipótese de trabalho que o mundo físico tem realidade objetiva (a Terra gira em torno do Sol, independentemente de estarmos percebendo os efeitos deste movimento), e a Física deveria se aproximar desta com suas teorias. Por isso, deveria ser independente de observadores. E de fato, na sua recém-construída e bem-sucedida Teoria da Relatividade Geral, observadores não têm papel essencial. Portanto, uma formulação mais fundamental da mecânica quântica deveria ser procurada. Nas palavras de Einstein:

” A teoria quântica contemporânea … constitui uma formulação ótima de [certas] conexões …

[mas] não oferece qualquer ponto de partida útil para desenvolvimentos futuros”.

Bohm então se propôs a procurar uma alternativa. Havia uma dificuldade, o famoso teorema de Von Neumann, mostrando a impossibilidade de uma dinâmica subjacente à mecânica quântica com variáveis escondidas. Físicos da época viam este teorema como definitivo. Entretanto, Bohm percebeu que as premissas deste teorema eram excessivamente restritivas. Logo descobriu como construir teorias compatíveis com os resultados da Mecânica Quântica, e elaborou sua teoria alternativa, envolvendo variáveis escondidas (a posição inicial da partícula). Nada melhor que introduzir sua nova teoria através das palavras do brilhante físico irlandês John Stewart Bell: “A cinemática do mundo, nesta visão ortodoxa (Copenhaguen), é dada por uma função de onda para a parte quântica e variáveis clássicas – variáveis com realidade factual – para a parte clássica: (ψ (t ,q . . .),X(t ) . . .). Os X’s são de alguma maneira macroscópicos. Isto não é dito muito explicitamente. A dinâmica também não é formulada de forma bastante precisa. Ela inclui uma equação de Schrödinger para a parte quântica e algum tipo de mecânica clássica para a parte clássica, e receitas de ’colapso’ para a interação entre elas. Parece-me que a única esperança de precisão para a cinemática dual (ψ,x) é omitir completamente esta separação matreira e deixar que ambos ψ  e x se refiram ao mundo inteiro. Então os x’s não devem ficar confinados a uma vaga escala macroscópica, mas devem ser estendidos a todas as escalas.”

Assim, na nova teoria, as posições dos objetos quânticos teriam realidade independente da observação, e seriam elementos essenciais na descrição dos fenômenos quânticos. Portanto, além da equação de Schrödinger que descreve a evolução da onda quântica, deveria haver uma nova equação que descrevesse a evolução da posição das partículas quânticas. De fato, o físico francês Louis de Broglie já havia proposto este tipo de equação ainda em 1927. Bohm, sem conhecimento do trabalho de de Broglie, formulou equações equivalentes. Na formulação de de Broglie, a já conhecida corrente construída com a função de onda que satisfaz uma lei de conservação derivada da equação de Schrödinger deveria ser identificada com a velocidade da partícula. Assim, resolvendo-se a equação de Schrödinger e tendo a função de onda, teríamos sua corrente associada e, portanto, a velocidade das partículas quânticas em todos os pontos. Para saber a trajetória individual da partícula teríamos que saber sua posição inicial. Como não a conhecemos, e como para obtê-la teríamos que fazer medidas que interfeririam com o sistema original, esta seria a variável escondida da teoria. Entretanto, se a distribuição de posições iniciais for dada pela pelo módulo da função de onda ao quadrado no tempo inicial, |ψ(x,t=0)|² , todas as previsões estatísticas da mecânica quântica são recuperadas. Bohm mostrou que esta lei de evolução pode ser entendida como uma modificação da lei de Newton onde, além dos potenciais usuais das forças clássicas V(x,t), um novo potencial de forças apareceria naturalmente advindo da função de onda, o chamado potencial quântico Q(x,t), que seria o responsável por todos os efeitos estranhos da mecânica quântica. Quando este potencial é desprezível frente os potenciais clássicos, recuperamos a mecânica clássica. Assim, a mecânica clássica seria um caso limite da uma mecânica mais geral, a mecânica quântica, e o seu limite de aplicabilidade estaria precisamente bem definido. Não existem duas mecânicas, nem tampouco dois mundos, o clássico e o quântico. Há apenas o mundo quântico e sua mecânica.

A física da interferência quântica, descrita na figura 1, pode ser entendida de maneira simples segundo esta interpretação. A partícula quântica entra de fato por uma das fendas, mas a função de onda passa pelas duas e informa a partícula sobre a outra fenda através do potencial quântico. Na informação que é passada continuamente à partícula, estão dados sobre o tamanho e separação das fendas, a possível existência de detectores, filtros, e tudo o mais que for relevante para o seu movimento. Numa imagem proposta pelo próprio Bohm, a situação é análoga à de um veículo guiado por controle remoto: a onda que sai do controle remoto informa o veículo sobre a direção que ele deve seguir, mas a energia que move o veículo vem do combustível que faz seu motor funcionar. A figura 2 abaixo mostra as trajetórias calculadas. Notem os saltos dados pelas partículas na região onde elas estão livres. Vê-se que sua distribuição no anteparo final descreve uma figura de interferência perfeita, como deveria. Como a função de onda é nula na linha que divide o artefato ao meio, podemos afirmar, com certeza, contrariamente à teoria usual, que as partículas registradas na parte de cima do anteparo final vieram da fenda de cima, e analogamente para as de baixo, já que elas não podem cruzar a linha central. Esta informação adicional da teoria, entretanto, não tem poder preditivo nem pode ser testada.

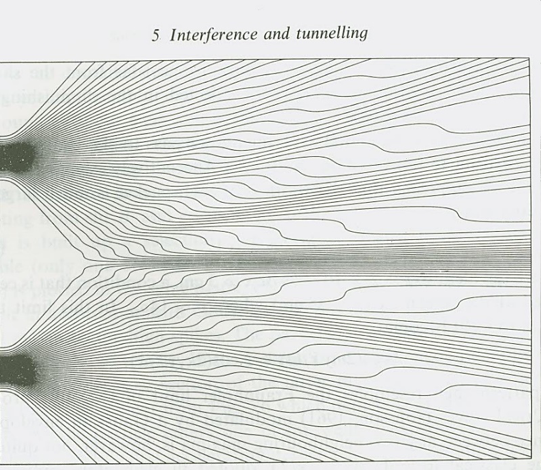
Vimos que o experimento de interferência quântica, quando analisado segundo a interpretação de Copenhaguen, implica na impossibilidade de se falar sobre trajetórias em mecânica quântica independentemente do ato de observação. Entretanto, através da teoria de de Broglie e Bohm, as trajetórias relativas àquele experimento puderam ser calculadas de forma consistente e expostas de maneira explícita. Isto mostra que a impossibilidade das trajetórias quânticas não é uma conclusão imposta a nós por fatos experimentais, como é dito em inúmeros cursos e livros didáticos, mas é, outrossim, consequência de uma escolha deliberada de pressupostos teóricos e filosóficos que não somos, de maneira alguma, forçados a aceitar. Se as trajetórias quânticas realmente existem, ainda não temos condições de decidir, mas a teoria de de Broglie-Bohm mostra que é possível, sim, conjecturar sobre sua existência e estudar suas propriedades. A inexorável impossibilidade de sequer poder falar sobre elas é apenas mais um dos tantos dogmas que permeiam a mecânica quântica.

Entretanto, a nova dinâmica quântica é bastante peculiar. Nesta nova teoria, as probabilidades aparecem devido ao desconhecimento sobre as posições iniciais das partículas quânticas, que possuem realidade objetiva e que estão sujeitas à ação à distância. Trata-se, portanto, de uma teoria realista e explicitamente não local, que dava conta de todos os resultados experimentais até então obtidos. Suas propriedades básicas são:

1. O potencial quântico Q é altamente dependente do ambiente por onde a partícula quântica circula (como vimos no caso da interferência quântica) e, no caso das funções de onda ditas emaranhadas, é altamente não local: num sistema de muitas partículas quânticas, a trajetória de qualquer uma delas depende instantaneamente da posição de todas as outras, por mais distante que estejam, formando um todo indissociável. Portanto, o potencial quântico não tem paralelo com os potenciais da mecânica clássica. A não localidade desagradou a Einstein.
2. Probabilidades não são essenciais na teoria, são apenas uma ferramenta auxiliar, como na mecânica clássica, consequência da nossa ignorância sobre as posições iniciais das partículas quânticas.
3. É uma teoria que assume uma realidade objetiva, mas apresenta as mesmas previsões estatísticas que a interpretação de Copenhaguen, essencialmente por causa da presença do Q não local.

Veremos mais adiante as repercussões desta nova teoria quântica e suas consequências para a Física.

A perseguição do McCartyismo e a vinda ao Brasil

Como já vimos, Bohm tinha ligações com o Partido Comunista Americano. Por isso, na época sinistra do MacCartyismo, foi chamado a depor no congresso, mas evocou a quinta emenda (para não incriminar seus amigos e colegas). Foi preso por um dia, solto sob fiança, e depois a Suprema Corte o inocentou por não haver crime contra ele. Foi afastado de Princeton, e depois não teve seu contrato renovado, uma página cinzenta da história desta universidade. Einstein e Oppenheimer articularam para ele vir para o Brasil, com ajuda dos físicos brasileiros Jayme Tiomno, José Leite Lopes, entre outros.

Bohm ficou no Brasil de 1951 a 1955. Ao chegar, os EUA apreenderam seu passaporte. Para então poder viajar, Bohm pediu a nacionalidade brasileira, mas perdeu a cidadania americana. Foram anos de angústia, não só por estar exilado, vendo o arbítrio do McCartyismo imperando nos EUA, mas também por estar recebendo várias críticas ao seu trabalho de alguns dos fundadores da mecânica quântica. O establishment não aceitava críticas à abordagem padrão dos fenômenos quânticos, o que se tornou um pesadelo para muitos físicos questionadores dos fundamentos da Mecânica Quântica, até recentemente (veja a referência 4). Um exemplo desta atitude é o comentário do físico belga Leon Rosenfeld, colaborador de Bohr, a respeito das discussões internas em relação a interpretação de Copenhaguen: “Não somente [. . . ] é fútil falar de duas escolas de Copenhaguen; mas é mesmo errado falar de uma escola de Copenhaguen; nunca existiu algo deste tipo e espero que nunca exista. A única distinção está entre físicos que entendem a mecânica quântica e aqueles que não a entendem.”

Neste período, Bohm respondeu a muitas críticas e questões pendentes da nova teoria que não haviam sido resolvidas por de Broglie na sua formulação original. Entre outras coisas, forneceu uma descrição precisa do processo de medida e observação sem precisar fazer referências a um mundo clássico externo ao mundo quântico. Respondeu também a importantes críticas do físico austríaco Wolfgang Pauli, uma delas com uma sonora bronca por Pauli não estar lendo suas respostas (Pauli era conhecido por seu estilo áspero, grosseiro e mordaz, é portanto surpreendente vê-lo na situação reversa): “Se eu escrever um artigo tão “curto” que você o leia, então não posso responder a todas as suas objeções. Se eu responder a todas as suas objeções, então o artigo será muito “longo” para você ler. Eu realmente acho que é seu dever ler esses artigos cuidadosamente.” Pauli finalmente leu as respostas de Bohm, e reconheceu que a nova teoria era perfeitamente consistente com todos os fenômenos quânticos. Entretanto, por não trazer nenhum resultado experimental novo, considerou-a inútil.

Evidentemente Bohm obteve o apoio de de Broglie e de seu aluno Jean-Pierre Vigier, como também de Jayme Tiomno, com o qual publicou uma artigo.

A saida do Brasil, o rompimento com o comunismo e com a sua interpretação causal, e a ida para a Inglaterra

Como visto acima as reações dos fundadores da Mecânica Quântica em relação à sua nova teoria não foram boas. A maioria considerou-a inútil por não trazer nenhum efeito diferente da Mecânica Quântica, e por ser difícil de construir sua generalização relativística. Assim, deixou de lado provisoriamente sua nova teoria quântica.

Em 1957 foi divulgado o relatório de Khrushchev sobre os crimes de Stalin, o que fez Bohm abandonar o comunismo. Saiu do Brasil para Israel e chegou à Inglaterra (Universidade de Bristol) em 1957. Ficou por lá 3 anos, quando trabalhou com seu aluno Yakir Aharonov, com quem realizou um dos seus artigos mais famosos, descrevendo o que passou a ser conhecido como efeito Aharonov-Bohm. Na Eletrodinâmica Clássica, os campos elétrico e magnético são as quantidades que podem concretamente ser medidas em experimentos. Eles podem ser obtidos matematicamente do chamado potencial vetor eletromagnético, mas este é inobservável pois só se manifesta através dos campos elétrico e magnético. Entretanto, na mecânica quântica, como mostrado por Aharonov e Bohm, o potencial eletromagnético induz efeitos físicos mensuráveis em partículas quânticas, modificando figuras de interferência conhecidas, mesmo nas regiões onde os campos elétrico e magnético são nulos. Este foi um resultado de grande importância para duas teorias fundamentais da Natureza: o Eletromagnetismo e a Mecânica Quântica, e medido experimentalmente 3 décadas depois.

Nas palavras do físico austríaco Victor Weisskopf: “A primeira reação a este artigo foi que ele está errado, a segunda que ele é óbvio”.

A retomada da teoria quântica de Bohm-de Broglie

Em 1961 Bohm adquiriu uma posição permanente no Birkbeck College em Londres. A partir de então, o interesse em sua formulação da mecânica quântica foi renovado com a entrada em cena de novos pesquisadores: Basil Hiley, Chris Dewdney, Peter Holland, entre outros. A nova teoria foi aplicada a diversas situações físicas, permitindo uma compreensão muito mais ampla de vários fenômenos quânticos, e permitindo aproximações bem mais precisas para determinados fenômenos complexos do que as que se obtém na interpretação de Copenhaguen. Ou seja, mesmo sem dar resultados experimentais novos até aquele momento, a nova abordagem permitia a criação de novos métodos de cálculo antes inexplorados.

Nesta época entra em cena John Bell, um dos raros físicos de sua geração a chegar ao mesmo nível de profundidade de compreensão da mecânica quântica que seus fundadores, ou mesmo ir além. Bell considerou que a simples constituição da alternativa apresentada por Bohm já representava, por si própria, um evento de capital importância para toda a teoria quântica, o qual precisaria ser analisado com muito cuidado. Nas suas palavras: “Em 1952, vi o impossível sendo feito. Foi nos artigos de David Bohm. … A subjetividade da versão ortodoxa, a referência necessária ao “observador” poderia ser eliminada. . . . Mas por que então Born não me contou sobre essa “onda piloto”? Talvez apenas para apontar o que haveria de errado com ela? Por que von Neumann não considerou isso? . . .Por que a teoria da onda piloto é ignorada nos livros texto? Não deveria ser ensinada, não como o único caminho, mas como um antídoto para a complacência prevalecente? Para nos mostrar que a imprecisão, subjetividade e indeterminismo, não nos são forçados por fatos experimentais, mas por uma escolha teórica deliberada? … Eu sempre senti, desde então, que as pessoas que não compreenderam as ideias desses artigos. . . e infelizmente elas permanecem a maioria . . . estão em desvantagem em qualquer discussão sobre o significado de mecânica quântica.”

Um problema fundamental que Bell resolveu estudar na teoria de Bohm-de Broglie era a sua não localidade. Seria possível construir uma teoria de variáveis escondidas local tão bem sucedida quanto a teoria de Bohm? Depois de muitas tentativas frustradas, Bell começou a indagar se a não localidade era uma necessidade da teoria quântica e passou a investigar esta possibilidade. Foi assim que surgiram os famosos teoremas de Bell. Ele mostrou que em qualquer teoria física local, certas probabilidades de resultados experimentais de eventos sem conexão causal deveriam satisfazer certas desigualdades que a Mecânica Quântica não satisfaz. Portanto a Mecânica Quântica é essencialmente não local. Experimentos foram realizados e evidenciaram que as desigualdades de Bell são efetivamente violadas, ou seja, a Natureza é efetivamente não local! Este é um dos resultados mais importantes do século XX, que fala sobre um aspecto fundamental da Natureza, independentemente das interações que nela se processam. Como disse jocosamente o físico suíço Nicolas Gisin: “Com Bell foi inaugurada a metafísica experimental!”

A teoria de Bohm é explicitamente não-local, e esta não localidade está explicitada quantitativamente no potencial quântico, o que para Bell é um dos méritos da teoria. Ele então desenvolve a teoria de Bohm dando contribuições significativas, tais como acomodando de maneira simples o spin e propondo generalizações relativísticas.

David Bohm além da Física

O pensamento de David Bohm nunca ficou restrito aos problemas da Física. Ele procurou estender a visão de mundo que emergia das suas formulações para os outros ramos do conhecimento: filosofia, biologia, neurociência, psicologia e arte. Para isso, dialogou com várias linhas de pensamento, não só influenciando-as, como também retroalimentando seu pensamento físico com o que aprendia ouvindo as outras áreas. Exemplos são suas conversas com o filósofo indiano Jiddu Krishnamurti, ou com o neurocientista tcheco Karl Pribram.

Como vimos, as funções de onda emaranhadas implicam num potencial quântico Q não local. Neste caso, sistemas físicos compostos por partículas ou subsistemas arbitrariamente distantes estariam todos conectados. Esta é uma expressão da indivisibilidade quântica tão enfatizada por Bohr, mas apenas em palavras, que Bohm denominou “totalidade”, e que agora poderia ser investigada e ampliada na nova teoria através das propriedades do potencial quântico. Na sua teoria, a função de onda, através do potencial quântico, guia as estruturas físicas (campos ou partículas), e contem todas as informações relativas a todo o sistema e seu entorno, guiando cada subsistema, mas estruturando a totalidade. Isto levou-o à noção de ordem implicada e explicada (as estruturas físicas que nos aparecem concretamente sendo a ordem explicada, e a função de onda, definida num espaço abstrato multi-dimensional, o chamado espaço das configurações, constituindo a ordem implicada). Para entender esta noção de ordem implicada e explicada, Bohm gostava de fazer uma analogia com um filme que ele viu na BBC, onde uma gota de tinta num cilindro cheio de glicerina desaparecia ao se fazer o cilindro girar para um lado, mas reaparecia ao se fazer o cilindro rodar no sentido contrário.

Ao final da vida Bohm propunha que “meaning”, mantendo a palavra em inglês, já que ela tem o duplo sentido de “significado” e “intenção”, é a essência da realidade. Se nos restringirmos ao domínio da mente, ou da consciência, esta afirmação não soa tão estranha, mas como Bohm observa, o significado que damos às coisas e as intenções que impulsionam nossos atos emergem, na maior parte das vezes, de forma espontânea, resultantes de toda a nossa história e relações com o ambiente (não só como indivíduo, mas também como espécie animal). Entretanto, se examinarmos a dinâmica quântica de um elétron na formulação Bohmiana, a situação é muito parecida: a função de onda, contendo todas as informações, “significados” e “intenções” da totalidade que contem o elétron, guia a partícula através do potencial quântico. Ou seja, mesmo um elétron tem um certo nível primário de consciência, e é indissociável deste. A diferença é que o elétron não tem consciência de ter consciência (assim parece). Para sustentar suas afirmações, Bohm defendia que as causas eficiente e material de Aristóteles utilizadas pela Física, em detrimento das causas formal e final, não podiam dar conta dos fenômenos quânticos, como Bohr já havia observado. A única maneira de recuperar alguma causalidade para a Mecânica Quântica seria trazer da volta as causas formal e final, unidas numa só. Seria este exatamente o papel da função de onda na mecânica Bohmiana: ser portadora da causa formal-final. A Natureza então seria composta de “meaning” (função de onda), energia (campos e partículas) e, em última análise, autoconsciência. Perguntado sobre o “meaning” do Universo, Bohm responde: o Universo não tem “meaning”, ele é “meaning”.

Os últimos anos e seu legado

Nos anos 80, Bohm recebeu ofertas de emprego nos EUA, que ofereceram de volta a nacionalidade americana caso ele renunciasse ao comunismo. Bohm respondeu em carta que não era mais comunista, mas as autoridades americanas queriam que isso fosse tornado público. Percebendo que estavam querendo usá-lo como instrumento de propaganda política, Bohm recusou. Como consequência, foi-lhe negado o visto de trabalho e ele não pode voltar a trabalhar no seu país de nascimento. Mais para o fim da vida, as autoridades americanas devolveram-lhe a cidadania sem qualquer condição, mas já não havia mais posições para ele nos EUA. Continuou na Inglaterra, até falecer em 1992.

Além de influenciar vários outros setores do pensamento, o legado de David Bohm à Física é imenso, em todas as áreas. Está sendo publicado um livro contendo as inúmeras consequências de sua teoria quântica para várias áreas da Física: “Applied Bohmian Mechanics: From Nanoscale Systems to Cosmology”, onde vários autores relatam a utilidade e versatilidade da teoria em várias áreas da Ciência, da Química Quântica à Cosmologia Quântica.

No que diz respeito à Cosmologia Quântica, área na qual trabalho, logo de início, nos deparamos com um impasse em relação a interpretação de Copenhaguen. Como vimos, ela exige um mundo clássico externo ao sistema quântico para que os fatos concretos e os conceitos clássicos relativos a este sistema tenham sentido e existência. Ora, se o sistema a ser quantizado é a totalidade de todos os sistemas físicos, o Universo, então não pode haver mundo clássico externo a este que possa dar sentido à teoria. Desta forma, por definição, a própria concepção de cosmologia quântica não faz sentido no escopo desta interpretação. Seria como falar da biologia da matéria inanimada. Felizmente, com a teoria de Bohm-de Broglie, um Universo quântico faz sentido. Aplicando esta teoria aos modelos padrões cosmológicos que descrevem o Universo observado, obtivemos um universo eterno sem começo do tempo, que se contrai classicamente de um volume muito grande, chegando a um mínimo, quando então sua contração é interrompida pela ação do potencial quântico, que funciona como um potencial repulsivo, superando a imensa atração gravitacional neste momento. Se não fosse a ação deste potencial quântico, o Universo colapsaria totalmente num único ponto e seria destruído. A partir do seu tamanho mínimo, o Universo se expande, até atingir o limite clássico, onde a evolução clássica da cosmologia padrão acontece, com a formação de estrelas e galáxias. Pode-se mostrar que o potencial quântico só é relevante perto do raio mínimo. Assim, efeitos quânticos podem evitar o colapso total do Universo, tornando-o eterno. Efeitos desta fase quântica estão atualmente sendo estudados para saber se eles podem implicar em fatos passíveis de observação. Se for este o caso, teremos uma instância onde efeitos da teoria de Bohm-de Broglie podem ser medidos sem que haja uma contrapartida vinda da interpretação de Copenhaguen. Isto seria, portanto, o efeito físico característico que Bohm tanto procurava dentro da sua teoria. Se isso acontecer, seja através da Cosmologia ou de outra área da Física ainda inexplorada, será mais um exemplo onde novas formas de pensar os mesmos fenômenos, que em um primeiro momento podem parecer banais ou inúteis, podem levar a desdobramentos surpreendentes, e a novos e fascinantes caminhos a percorrer.

“O Universo começa a parecer-se mais com uma grande ideia do que com uma grande máquina.”

David Bohm

Recomendações de leitura:

• “Quantum Implications: Essays in Honour of David Bohm”, editado por B. J. Hiley e F. David Peat, (Routledge, Londres, 1991).
• “Causality and Chance in Modern Physics”, por David Bohm (University of Pennsylvania Press, Filadélfia, 1957).
• “Wholeness and the Implicate Order”, por David Bohm, (Ark Paperbacks, Londres, 1980).
• “The Quantum Dissidents: Rebuilding the Foundations of Quantum Mechanics (1950-1990)”, por Olival Freire Jr. (Springer-Verlag, Berlim, 2015).
• “Teorias e Interpretações da Mecânica Quântica”, por Nelson Pinto Neto (Editora Livraria da Física, USP, São Paulo, 2010).